（本小题满分12分）某商店预备在
一个月内分批购入每张价值为20元的书桌共36台，每批都购入x台（x是
正整数），且每批均需付运费4元，储存购入的书桌一个月所付的保管费与每批购入书桌的总价值（不含运费）成正比，若每批购入4台，则该月需用去运费和保管费共52元，现在全月只有48元资金可以用于支付运费和保管费.
（1）求该月需用去的运费和保管费的总费用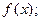
（2）能否恰
当地
安排每批进货的数量，使资金够用？写出你的结论，
选修4-2：矩阵与变换
已知直线
，若矩阵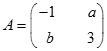
所对应的变换
把直线
变换为它自身。
（Ⅰ）求矩阵A；
（Ⅱ）求矩阵A的逆矩阵.
已知函数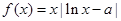
，
．
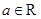（Ⅰ）当
时，试求
的单调区间；
（Ⅱ）若对任意的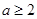
，方程
恒有三个不等根，试求实数b的取值范围．
已知椭圆
的中心为
，右顶点为
，在线段
上任意选定一点
，过点
作与
轴垂直的直线交
于
两点.
（Ⅰ）若椭圆的长半轴为2，离心率
，
（ⅰ）求椭圆的标准方程；
（ⅱ）若
，点
在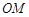
的延长线上，且
成等比数列，试证明直线
与相切；
（Ⅱ）试猜想过椭圆
上一点
的切线方程的一种方法，再加以证明.
如图，已知四棱锥
的底面为菱形，
，
，
.
（Ⅰ）求证：
；
（Ⅱ）在线段AD上是否存在点Q，使得直线CQ和平面BCP所成角
的正弦值为
？若存在，请说明点Q位置；若不存在，请说明不存在的理由.
某个海边旅游景点，有小型游艇出租供游客出海游玩，收费标准如下：租用时间不超过2小时收费100，超过2小时的部分按每小时100收取（不足一小时按一小时计算）．现甲、乙两人独立来该景点租用小型游艇，各租一次．设甲、乙租用不超过两小时的概率分别为
，
；租用2小时以上且不超过3小时的概率分别为，，且两人租用的时间都不超过4小时．
（Ⅰ）求甲、乙两人所付费用相同的概率；
（Ⅱ）设甲、乙两人所付的费用之和为随机变量
，求的分布列与数学期望．