已知函数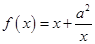 ,
,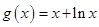 ,其中
,其中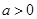 .
.
(1)若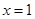 是函数
是函数 的极值点,求实数
的极值点,求实数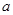 的值;
的值;
(2)若对任意的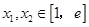 (
( 为自然对数的底数)都有
为自然对数的底数)都有 ≥
≥ 成立,求实数
成立,求实数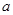 的取值范围.
的取值范围.
设函数f(x)=x2-mlnx,g(x)=x2-x+a.
(1)当a=0时,f(x)≥g(x)在(1,+∞),上恒成立,求实数m的取值范围;
(2)当m=2时,若函数h(x)=f(x)-g(x)在[1,3]上恰有两个不同的零点,求实数a的取值范围.
设f(x)=ax3+bx+c(a≠0)为奇函数,其图象在点(1,f(1))处的切线与直线x-6y-7=0垂直,导函数f′(x)的最小值为-12.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调增区间,并求函数f(x)在[-1,3]上的最大值和最小值.
如右图,由曲线 与直线
与直线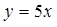 ,
, ,
,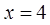 所围成平面图形的面积.
所围成平面图形的面积.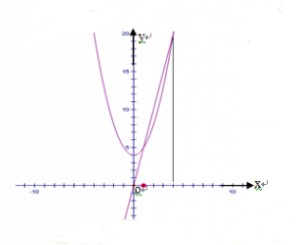
如图,在 中,
中,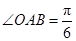 ,斜边
,斜边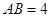 .
.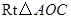 可以通过
可以通过 以直线
以直线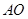 为轴旋转得到,且二面角
为轴旋转得到,且二面角 是直二面角.动点
是直二面角.动点 在斜边
在斜边 上.
上.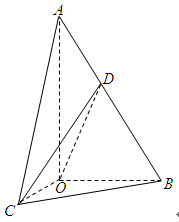
(1)求证:平面 平面
平面 ;
;
(2)求 与平面
与平面 所成角的最大角的正切值.
所成角的最大角的正切值.