在平面直角坐标系xOy中,已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x
-4)2+(y-5)2=4.
(1)若点M∈⊙ C1, 点N∈⊙C2,求|MN|的取值范围;
(2)若直线l过点A(4,0),且被圆C1截得的弦长为2  ,求直线l的方程;
,求直线l的方程;
(3)设P为平面上的点,满足:存在过点P的无数多对互相垂直的直线l1和l2,它们分别与圆C1和圆C2相交,且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,试求所有满足条件的点P的坐标。
2008年北京奥运会中国跳水梦之队取得了辉煌的成绩。据科学测算,跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动轨迹(如图所示)是一经过坐标原点的抛物线(图中标出数字为已知条件),且在跳某个规定动作时,正常情况下运动员在空中的最高点距水面 米,入水处距池边4米,同时运动员在距水面5米或5米以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误。
米,入水处距池边4米,同时运动员在距水面5米或5米以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误。
(Ⅰ)求抛物线的解析式;
(Ⅱ)某运动员按 (1)中抛物线运行,要使得此次跳水成功,他在空中调整好入水姿势时,距池边的水平距离至多应为多大?
(1)中抛物线运行,要使得此次跳水成功,他在空中调整好入水姿势时,距池边的水平距离至多应为多大?
已知函数 、
、 对任意实数
对任意实数 、
、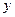 都满足条件
都满足条件
①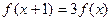 ,且
,且 ,和②
,和② ,且
,且 ,
,
(Ⅰ)求数列 、
、 的通项公式;(
的通项公式;( 为正整数)
为正整数)
(II)设 ,求数列
,求数列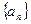 的前
的前 项和
项和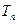 。
。
在 中,已知内角A、B、C成等差数列,边AC
中,已知内角A、B、C成等差数列,边AC 6。设内角
6。设内角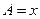 ,
, 的周长为
的周长为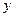 。
。
在 中,已知
中,已知 ,求边
,求边 的长及
的长及 的面积S。
的面积S。
某企业利用银行无息贷款,投资400万元引进一条高科技生产流水线,预计每年可获产品利润100万元。但还另需用于此流水线的保养、维修费用第一年10万元,以后每年递增5万元,问至少几年可收回该项投资?(即总利润不小于总支出)