(本小题满分12分)已知条件 (a>0)和条件
(a>0)和条件 ,
,
请选取适当的实数 的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题.则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题.则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
(本小题满分12分)
已知函数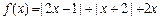 (
( ),
),
(Ⅰ)求函数 的最小值;
的最小值;
(Ⅱ)已知 ,命题p:关于x的不等式
,命题p:关于x的不等式 解集是空集;命题q:关于x的方程
解集是空集;命题q:关于x的方程 有实数根.若“p或q”为真,“p且q”为假,求实数m的取值
有实数根.若“p或q”为真,“p且q”为假,求实数m的取值 范围.
范围.
(本小题满分1 2分)
2分)
某市有A、B两所示范高中响应政府号召,对该市甲、乙两个教育落后地区开展支教活动.经上级研究决定:向甲地派出3名A校教师和2名B校教师,向 乙地派出3名A校教师和3名B校教师.由于客观原因,需从拟派往甲、乙两地的教师中各自任选一名互换支教地区.
乙地派出3名A校教师和3名B校教师.由于客观原因,需从拟派往甲、乙两地的教师中各自任选一名互换支教地区.
(Ⅰ)求互换后两校派往两地区教师人数不变的概率;
(Ⅱ)求互换后A校教师派往甲地人数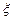 的分布列和数学期望
的分布列和数学期望 .
.
(本小题满分1 2分)
2分)
已知函数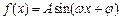 (
(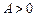 ,
,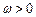 ,
,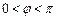
 )在
)在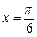 取得最大值2,方程
取得最大值2,方程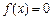 的两个根为
的两个根为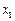 、
、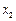 ,且
,且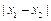 的最小值为
的最小值为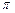 .
.
(Ⅰ)求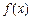 ;
;
(Ⅱ)将函数 图象上各点的横坐标压缩到原来的
图象上各点的横坐标压缩到原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数 的图象.当
的图象.当 时,函数
时,函数 (m、n∈R)的值域是
(m、n∈R)的值域是 ,求实数m、n的值.
,求实数m、n的值.
(本小题满分12分)
已知向量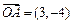 ,
, ,
,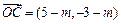 .
.
(Ⅰ)若点A、B、C能构成三角形,求实数m的取值范围;
(Ⅱ)若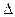 ABC为直角三角形,且
ABC为直角三角形,且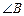 为直角,求实数m的值.
为直角,求实数m的值.
已知双曲线 的离心率为2,焦点到渐近线的距离为
的离心率为2,焦点到渐近线的距离为 .过
.过
 的直线
的直线 与双曲线C交于不同的两点
与双曲线C交于不同的两点 、
、 .
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)当 时,求直线
时,求直线 的方程;
的方程;
(Ⅲ)设 (
( 为坐标原点),求
为坐标原点),求 的取值范围.
的取值范围.