如图,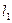 、
、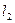 分别表示一种白炽灯和一种节能灯的费用
分别表示一种白炽灯和一种节能灯的费用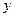 (费用=灯的售价+电费,单位:元)与照明时间
(费用=灯的售价+电费,单位:元)与照明时间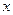 (小时)的函数图象,假设两种灯的使用寿命都是2000小时,照明效果一样。
(小时)的函数图象,假设两种灯的使用寿命都是2000小时,照明效果一样。
(1)根据图象分别求出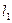 、
、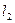 的函数关系式;
的函数关系式;
(2)当照明时间为多少时,两种灯的费用相等?
(3)小亮房间计划照明2500小时,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法(直接给出答案,不必写出解答过程)。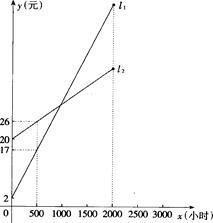
已知二次函数 的图象
的图象 经过
经过 ,
, 两点.
两点.
(1)求 对应的函数表达式;
对应的函数表达式;
(2)将 先向左平移1个单位,再向上平移4个单位,得到抛物线
先向左平移1个单位,再向上平移4个单位,得到抛物线 ,将
,将 对应的函数表达式记为
对应的函数表达式记为 ,求
,求 对应的函数表达式;
对应的函数表达式;
(3)设 ,在(2)的条件下,如果在
,在(2)的条件下,如果在 ≤x≤a内存在某一个x的值,使得
≤x≤a内存在某一个x的值,使得 ≤
≤ 成立,利用函数图象直接写出a的取值范围.
成立,利用函数图象直接写出a的取值范围.
阅读下面的材料:
小敏在数学课外小组活动中遇到这样一个问题:
如果α,β都为锐角,且 ,
, ,求
,求 的度数.
的度数.
小敏是这样解决问题的:如图1,把 ,
, 放在正方形网格中,使得
放在正方形网格中,使得 ,
, ,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰直角三角形,因此可求得
,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰直角三角形,因此可求得 ="∠ABC" =
="∠ABC" =
°.
请参考小敏思考问题的方法解决问题:
如果 ,
, 都为锐角,当
都为锐角,当 ,
, 时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=
时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON= ,由此可得
,由此可得 =______°.
=______°.
如图,AB为⊙O的直径,M为⊙O外一点,连接MA与⊙O交于点C,连接MB并延长交⊙O于点D,经过点M的直线l与MA所在直线关于直线MD对称.作BE⊥l于点E,连接AD,DE.
(1)依题意补全图形;
(2)在不添加新的线段的条件下,写出图中与∠BED相等的角,并加以证明.
在北京,乘坐地铁是市民出行时经常采用的一种交通方式.据调查,新票价改革政策的实施给北京市轨道交通客流带来很大变化.根据2015年1月公布的调价后市民当时乘坐地铁的相关调查数据,制作了以下统计表以及统计图.
根据以上信息解答下列问题:
(1)补全扇形图;
(2)题目所给出的线路中,调价后客流量下降百分比最高的线路是,调价后里程x(千米)在范围内的客流量下降最明显.对于表中客流量不降反增而且增长率最高的线路,如果继续按此变化率增长,预计2016年1月这条线路的日均客流量将达到万人次;(精确到0.1)
(3)小王同学上学时,需要乘坐地铁15.9公里到达学校,每天上下学共乘坐两次.问调价后小王每周(按5天计算)乘坐地铁的费用比调价前多支出元.(不考虑使用市政一卡通刷卡优惠,调价前每次乘坐地铁票价为2元)
如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.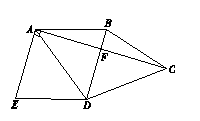
(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长.