已知梯形 中,
中, ∥
∥ ,且
,且 ,
, ,
, 。
。
⑴如图, 为
为 上的一点,满足
上的一点,满足 ,求
,求 的长;
的长;
⑵如果点 在
在 边上移动(点
边上移动(点 与点
与点 、
、 不重合),且满足
不重合),且满足 ,
, 交直线
交直线 于点
于点 ,同时交直线
,同时交直线 于点
于点 。
。
①当点 在线段
在线段 的延长线上时,设
的延长线上时,设 ,
, ,求
,求 关于
关于 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
②写 时,写出
时,写出 的长(不必写解答过程)
的长(不必写解答过程)
如图,菱形ABCD中,∠A=60°,对角线BD=4cm,求该菱形的周长.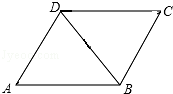
如图,平行四边形ABCD中,试用三种不同的方法将平行四边形分成面积相等的四部分.
如图,直线y=﹣ x+b交x轴于点A,交直线y=
x+b交x轴于点A,交直线y= x于点B(2,m),矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(﹣2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
x于点B(2,m),矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(﹣2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
(1)求b,m的值;
(2)矩形CDEF运动t秒时,直接写出C、D两点的坐标(用含t的代数式表示);
(3)当点B在矩形CDEF的一边上时,求t的值.
某市从今年1月1日起调整居民用天燃气价格,每立方米天燃气价格上涨25%.小颖家去年12月份的燃气费是96元.今年小颖家将天燃气热水器换成了太阳能热水器,5月份的用气量比去年12月份少10m3,5月份的燃气费是90元.求该市今年居民用气的价格?
已知:P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足.
求证:AP=EF.