(本题11分)如图1,抛物线y=ax2+bx+c(a≠0)的顶点为(1,4),交x轴于A、B,交y轴于D,其中B点的坐标为(3,0)
(1)求抛物线的解析式
(2)如图 2,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则
2,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则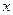 轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐
轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐 标;若不存在,请说明理由.
标;若不存在,请说明理由.
(3)如图3,抛物线上是否存在一点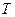 ,过点
,过点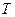 作
作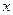 轴的垂线,垂足为
轴的垂线,垂足为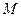 ,过点
,过点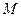 作直线
作直线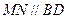 ,交线段
,交线段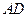 于点
于点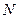 ,连接
,连接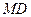 ,使
,使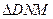 ~
~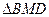 ,若存在,求出点
,若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.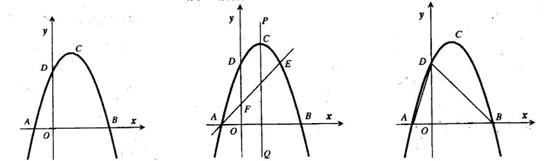 图1 图2
图1 图2  图3
图3
已知如图:平行四边形ABCD中, ,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
(1)求证:GH∥平面CDE;
(2)若 ,求四棱锥F-ABCD的体积.
,求四棱锥F-ABCD的体积.
我区高三期末统一测试中某校的数学成绩分组统计如下表:
| 分组 |
频数 |
频率 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
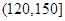 |
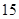 |
 |
| 合计 |
 |
 |
(1)求出表中 、
、 、
、 、
、 的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
(2)若我区参加本次考试的学生有600人,试估计这次测试中我区成绩在 分以上的人数;
分以上的人数;
(3)若该校教师拟从分数不超过60的学生中选取2人进行个案分析,求被选中2人分数不超过30分
的概率.
已知函数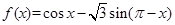 .
.
求函数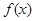 的最小正周期和值域;
的最小正周期和值域;
若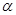 是第二象限角,且
是第二象限角,且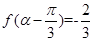 ,试求
,试求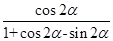 的值.
的值.
设椭圆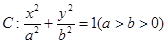 的左、右焦点分别为
的左、右焦点分别为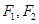 ,
,
上顶点为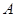 ,在
,在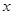 轴负半轴上有一点
轴负半轴上有一点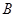 ,满足
,满足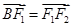 ,且
,且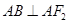 .
.
(Ⅰ)求椭圆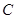 的离心率;
的离心率;
(Ⅱ)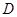 是过
是过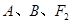 三点的圆上的点,
三点的圆上的点,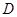 到直线
到直线 的最大距离等于椭圆长轴的长,求椭圆
的最大距离等于椭圆长轴的长,求椭圆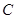 的方程;
的方程;
(Ⅲ)在(Ⅱ)的条件下,过右焦点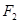 作斜率为
作斜率为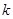 的直线
的直线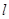 与椭圆
与椭圆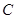 交于
交于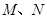 两点,线段
两点,线段 的中垂线与
的中垂线与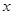 轴相交于点
轴相交于点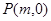 ,求实数
,求实数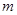 的取值范围.
的取值范围.
已知数列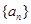 的前
的前 项和为
项和为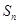 ,且
,且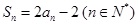 ,
,
数列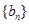 满足
满足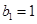 ,且点
,且点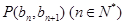 在直线
在直线 上.
上.
(Ⅰ)求数列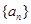 、
、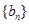 的通项公式;
的通项公式;
(Ⅱ)求数列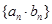 的前
的前 项和
项和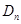 ;
;
(Ⅲ)设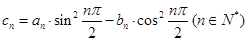 ,求数列
,求数列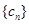 的前
的前 项和
项和 .
.