已知函数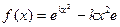 (
(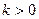 )(
)(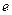 为自然对数的底数)
为自然对数的底数)
(1)求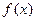 的极值
的极值
(2)对于数列 ,
,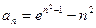 (
(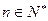 )
)
① 证明:
② 考察关于正整数
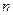 的方程
的方程 是否有解,并说明理由
是否有解,并说明理由
在一个交通拥挤及事故易发生路段,为了确保交通安全,交通部门规定,在此路段内的车速v(单位:km/h)的平方和车身长 (单位:m)的乘积与车距d成正比,且最小车距不得少于半个车身长.假定车身长均为
(单位:m)的乘积与车距d成正比,且最小车距不得少于半个车身长.假定车身长均为 (单位:m)且当车速为50(km/h)时,车距恰为车身长,问交通繁忙时,应规定怎样的车速,才能使在此路段的车流量Q最大?(车流量=
(单位:m)且当车速为50(km/h)时,车距恰为车身长,问交通繁忙时,应规定怎样的车速,才能使在此路段的车流量Q最大?(车流量= )
)
已知函数 (其中
(其中 ) ,点
) ,点

 从左到右依次是函数
从左到右依次是函数 图象上三点,且
图象上三点,且 .
.
(1)证明: 函数 在
在 上是减函数;
上是减函数;
(2)求证:⊿ 是钝角三角形;
是钝角三角形;
(3)试问,⊿ 能否是等腰三角形?若能,求⊿
能否是等腰三角形?若能,求⊿ 面积的最大值;若不能,请说明理由.
面积的最大值;若不能,请说明理由.
已知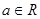 ,讨论函数
,讨论函数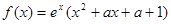 的极值点的个数
的极值点的个数
已知曲线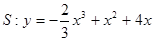 及点
及点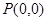 ,求过点
,求过点 的曲线
的曲线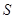 的切线方程.
的切线方程.
已知函数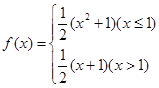 判断f(x)在x=1处是否可导?
判断f(x)在x=1处是否可导?