已知函数f(x)=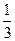 x3-ax2+(a2-1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y-3=0.
x3-ax2+(a2-1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y-3=0.
(1)求a,b的值;
(2 )求函数f(x)的单调区间,并求出f(x)在区间[-2,4]上的最大值.
)求函数f(x)的单调区间,并求出f(x)在区间[-2,4]上的最大值.
求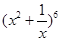 展开式中的常数项.
展开式中的常数项.
已知各项均为正数的两个无穷数列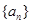 、
、 满足
满足 .
.
(Ⅰ)当数列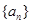 是常数列(各项都相等的数列),且
是常数列(各项都相等的数列),且 时,求数列
时,求数列 的通项公式;
的通项公式;
(Ⅱ)设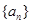 、
、 都是公差不为0的等差数列,求证:数列
都是公差不为0的等差数列,求证:数列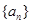 有无穷多个,而数列
有无穷多个,而数列 惟一确定;
惟一确定;
(Ⅲ)设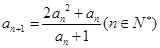 ,
,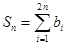 ,求证:
,求证: .
.
已知 是实数,函数
是实数,函数 ,
, 和
和 ,分别是
,分别是 的导函数,若
的导函数,若 在区间
在区间 上恒成立,则称
上恒成立,则称 和
和 在区间
在区间 上单调性一致.
上单调性一致.
(Ⅰ)设 ,若函数
,若函数 和
和 在区间
在区间 上单调性一致,求实数
上单调性一致,求实数 的取值范围;
的取值范围;
(Ⅱ)设 且
且 ,若函数
,若函数 和
和 在以
在以 为端点的开区间上单调性一致,求
为端点的开区间上单调性一致,求 的最大值.
的最大值.
如图,已知椭圆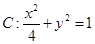 的上、下顶点分别为
的上、下顶点分别为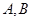 ,点
,点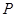 在椭圆上,且异于点
在椭圆上,且异于点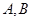 ,直线
,直线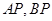 与直线
与直线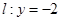 分别交于点
分别交于点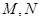 ,
,
(Ⅰ)设直线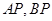 的斜率分别为
的斜率分别为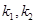 ,求证:
,求证: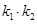 为定值;
为定值;
(Ⅱ)求线段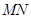 的长的最小值;
的长的最小值;
(Ⅲ)当点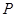 运动时,以
运动时,以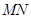 为直径的圆是否经过某定点?请证明你的结论.
为直径的圆是否经过某定点?请证明你的结论.
某商场在店庆一周年开展“购物折上折活动”:商场内所有商品按标价的八折出售,折后价格每满500元再减100元.如某商品标价为1500元,则购买该商品的实际付款额为1500×0.8-200=1000(元).设购买某商品得到的实际折扣率 .设某商品标价为
.设某商品标价为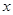 元,购买该商品得到的实际折扣率为
元,购买该商品得到的实际折扣率为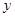 .
.
(Ⅰ)写出当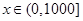 时,
时,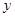 关于
关于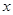 的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
(Ⅱ)对于标价在[2500,3500]的商品,顾客购买标价为多少元的商品,可得到的实际折扣率低于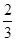 ?
?