(本小题满分12分) 已知函数 ,数列
,数列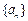 ,
, 满足条件:
满足条件: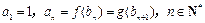 .
.
(1)求证:数列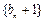 为等比数列;
为等比数列;
(2)令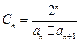 ,Tn是数列
,Tn是数列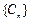 的前n项和,求使
的前n项和,求使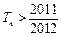 成立的最小的n值.
成立的最小的n值.
设函数 .
.
(1)当 时,求函数
时,求函数 在区间
在区间 内的最大值;
内的最大值;
(2)当 时,方程
时,方程 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值.
如图,椭圆 的长轴长为
的长轴长为 ,点
,点 、
、 、
、 为椭圆上的三个点,
为椭圆上的三个点, 为椭圆的右端点,
为椭圆的右端点, 过中心
过中心 ,且
,且 ,
, .
.
(1)求椭圆的标准方程;
(2)设 、
、 是椭圆上位于直线
是椭圆上位于直线 同侧的两个动点(异于
同侧的两个动点(异于 、
、 ),且满足
),且满足 ,试讨论直线
,试讨论直线 与直线
与直线 斜率之间的关系,并求证直线
斜率之间的关系,并求证直线 的斜率为定值.
的斜率为定值.
已知数列 满足
满足 ,向量
,向量 ,
, 且
且 .
.
(1)求证数列 为等差数列,并求
为等差数列,并求 通项公式;
通项公式;
(2)设 ,若对任意
,若对任意 都有
都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
如图,在直三棱柱 中,
中, ,
, ,且异面直线
,且异面直线 与
与 所成的角等于
所成的角等于 .
.
(1)求棱柱的高;
(2)求 与平面
与平面 所成的角的大小.
所成的角的大小.
2013年11月,青岛发生输油管道爆炸事故造成胶州湾局部污染.国家海洋局用分层抽样的方法从国家环保专家、海洋生物专家、油气专家三类专家库中抽取若干人组成研究小组赴泄油海域工作,有关数据见表1(单位:人)
海洋生物专家为了检测该地受污染后对海洋动物身体健康的影响,随机选取了 只海豚进行了检测,并将有关数据整理为不完整的
只海豚进行了检测,并将有关数据整理为不完整的 列联表,如表2.
列联表,如表2.
(1)求研究小组的总人数;
(2)写出表2中 、
、 、
、 、
、 、
、 的值,并判断有多大的把握认为海豚身体不健康与受到污染有关;
的值,并判断有多大的把握认为海豚身体不健康与受到污染有关;
(3)若从研究小组的环保专家和海洋生物专家中随机选 人撰写研究报告,求其中恰好有
人撰写研究报告,求其中恰好有 人为环保专家的概率.
人为环保专家的概率.
附:① ,其中
,其中 .
.
②
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |