请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四 个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱
个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱 形状的包装盒,E、
形状的包装盒,E、 F在AB上是被切去的等腰直角
F在AB上是被切去的等腰直角 三角形斜边的两个端点,设AE=FB=xcm.
三角形斜边的两个端点,设AE=FB=xcm.
(1)若广告商要求包装盒侧面积S(cm )最大,试问x
)最大,试问x 应取何值?
应取何值?
(2)若广告商要求包装盒容积V(cm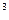 )最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.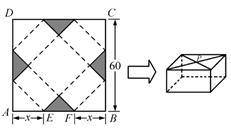
(本小题满分12分)椭圆 过点
过点 ,离心率为
,离心率为 ,左右焦点分别为
,左右焦点分别为 ,过点
,过点 的直线交椭圆于
的直线交椭圆于 两点。
两点。
(1)求椭圆 的方程;
的方程;
(2)当 的面积为
的面积为 时,求
时,求 的方程.
的方程.
(本小题满分12分)某学校有男老师45名,女老师15名,按照分层抽样的方法组建了一个4人的学科攻关小组。
(1)求某老师被抽到的概率及学科攻关小组中男、女老师的人数;
(2)经过一个月的学习、讨论,这个学科攻关小组决定选出2名老师做某项实验,方法是先从小组里选出1名老师做实验,该老师做完后,再从小组内剩下的老师中选1名做实验,求选出的2名老师中恰有1名女老师的概率.
(本题12分)如图,在四棱锥E-ABCD中,AB⊥平面BCE,DC⊥平面BCE,AB=BC=CE=2CD=2, ;
;
(1)求证:平面ADE⊥平面ABE;
(2)求三棱锥A-BDE的体积.
(本小题满分12分)已知函数 ,且当
,且当 时,
时, 的最小值为2,
的最小值为2,
(1)求 的值,并求
的值,并求 的单调递增区间;
的单调递增区间;
(2)先将函数 的图象上的点纵坐标不变,横坐标缩小到原来的
的图象上的点纵坐标不变,横坐标缩小到原来的 ,再将所得的图象向右平移
,再将所得的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,求方程
的图象,求方程 在区间
在区间 上所有根之和.
上所有根之和.
(本小题满分12分)设数列 的前n项和为
的前n项和为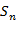 ,点
,点 均在函数y=x-2的图像上.
均在函数y=x-2的图像上.
(1)求数列 的通项公式;
的通项公式;
(2)求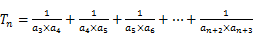 ;
;
(3)在(2)的条件下,求使得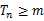 对所有
对所有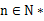 都成立的最大整数m.
都成立的最大整数m.