(本题12分)已知数列{an}中,a1=0,a2 =4,且an+2-3an+1+2an= 2n+1(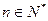 ),
),
数列{bn}满足bn=an+1-2an.
(Ⅰ)求证:数列{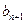 -
-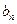 }是等比数列;
}是等比数列;
(Ⅱ)求数列{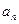 }的通项公式;
}的通项公式;
(Ⅲ)求 .
.
(本小题满分12分)某工厂的A、B、C三个不同车间生产同一产品的数量(单位:件)如下表所示. 质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测.
| 车间 |
A |
B |
C |
| 数量 |
50 |
150 |
100 |
(1)求这6件样品中来自A、B、C各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件商品来自相同车间的概率.
(本小题满分14分)设a为常数,且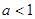 .
.
(1)解关于x的不等式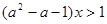 ;
;
(2)解关于x的不等式组 .
.
(本小题满分14分)如图,四棱柱 中,
中, ^底面ABCD,且
^底面ABCD,且 . 梯形ABCD的面积为6,且AD//BC,AD=2BC,
. 梯形ABCD的面积为6,且AD//BC,AD=2BC, . 平面
. 平面 与
与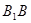 交于点E.
交于点E. 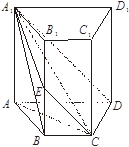
(1)证明:EC// ;
;
(2)求三棱锥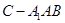 的体积;
的体积;
(3)求二面角 的大小.
的大小.
(本小题满分14分)
某家电生产企业根据市场调查分析,决定调整新产品生产方案,准备每周(按40个工时计算)生产空调器、彩电、冰箱共120台,且冰箱至少生产20台. 已知生产这些家电产品每台所需工时和每台产值如下表:
| 家电名称 |
空调器 |
彩电 |
冰箱 |
| 工时 |
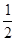 |
 |
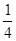 |
| 产值/千元 |
4 |
3 |
2 |
问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位)
(本小题满分14分)某商店根据以往某种玩具的销售记录,绘制了日销售量的频率分布直方图,如图所示,将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立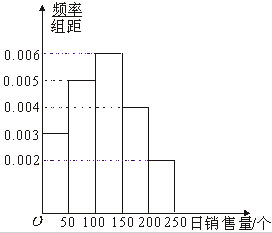
(1)估计日销售量的众数;
(2)求在未来连续3天里,有连续2天的日销售量都不低于100个且另一天的日销售量低于50个的概率;
(3)用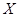 表示在未来3天里日销售量不低于100个的天数,求随机变量
表示在未来3天里日销售量不低于100个的天数,求随机变量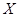 的分布列,期望
的分布列,期望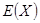 及方差
及方差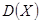 .
.