(本小题满分14分)已知数列{an}的前n项和为Sn,且an是Sn与2的等差中项,数列{bn}中,b1=1, 点P(bn,bn+1)在直线x-y+2=0上。
(1)求a1和a2的值; (2)求数列{an},{bn}的通项an和bn;
已知函数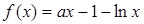
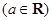 .
.
(1)当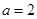 时,求函数
时,求函数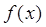 的单调区间;
的单调区间;
(2)若函数 在
在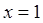 处取得极值,对
处取得极值,对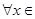
 ,
, 恒成立,求实数
恒成立,求实数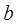 的取值范围;
的取值范围;
(3)当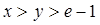 时,求证:
时,求证: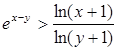 .
.
已知椭圆 经过点
经过点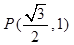 ,离心率
,离心率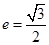 ,直线
,直线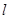 与椭圆交于
与椭圆交于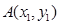 ,
, 两点,向量
两点,向量
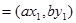 ,
,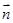
 ,且
,且 .
.
(1)求椭圆的方程;
(2)当直线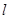 过椭圆的焦点
过椭圆的焦点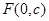 (
(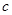 为半焦距)时,求直线
为半焦距)时,求直线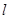 的斜率
的斜率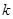 .
.
已知动圆 (
( )
)
(1)当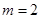 时,求经过原点且与圆
时,求经过原点且与圆 相切的直线
相切的直线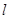 的方程;
的方程;
(2)若圆 恰在圆
恰在圆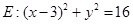 的内部,求实数
的内部,求实数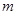 的取值范围.
的取值范围.
已知函数f(x)=ax2+bln x在x=1处有极值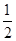 .
.
(1)求a,b的值;
(2)判断函数y=f(x)的单调性并求出单调区间.
已知复数 (
(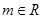 )
)
(1)若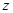 是实数,求
是实数,求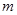 的值;
的值;
(2)若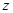 是纯虚数,求
是纯虚数,求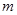 的值;
的值;
(3)若在复平面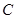 内,
内,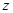 所对应的点在第四象限,求
所对应的点在第四象限,求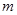 的取值范围。
的取值范围。