已知函数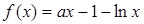
．
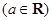（1）当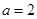
时，求函数
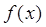的单调区间；
（2）若函数
在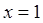
处取得极值，对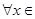
,
恒成立，求实数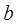
的取值范围；
（3）当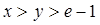
时，求证：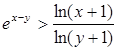
．
已知函数
．
（Ⅰ）若曲线
在点
处的切线与直线
垂直，求函数的单调区间；
（Ⅱ）若对于
都有
成立，试求
的取值范围；
（Ⅲ）记
．当
时，函数
在区间
上有两个零点，求实数
的取值范围．
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量
(升)关于行驶速度
(千米/小时)的函数解析式可以表示为:
已知甲、乙两地相距100千米．
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
判断命题“若
且
，则
”是真命题还是假命题，并证明你的结论．
数列
的前n项和记为
，已知
，
．
证明：（1）数列
是等比数列；
（2）
．
已知函数f(x)是(－∞，＋∞)上的增函数，a，b∈R．
(1)若a＋b≥0，求证：f(a)＋f(b)≥f(－a)＋f(－b)；
(2)判断(1)中命题的逆命题是否成立，并证明你的结论．