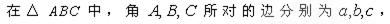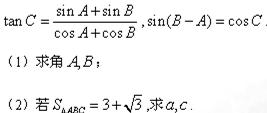已知函数f(x)是(－∞，＋∞)上的增函数，a，b∈R．
(1)若a＋b≥0，求证：f(a)＋f(b)≥f(－a)＋f(－b)；
(2)判断(1)中命题的逆命题是否成立，并证明你的结论．
（本小题满分10分）
如图6，AB是⊙O的弦，C、F是⊙O上的点，OC垂直于弦AB，过F点作⊙O的切线交AB的延长线于D，连结CF交AB于E点。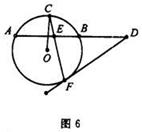
（I）求证：DE2=DB·DA.
（II）
若BE=1，DE=2AE，求DF的长.
（本题12分）
设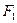
、
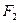分别是椭圆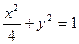
的左、右焦点，
是该椭圆上的一个动点，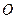
为坐标原点.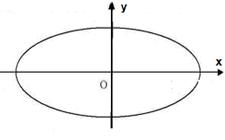 
（1）求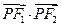
的取值范围;
（2）设过定点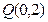
的直线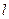
与椭圆交于不同的两点M、N，且∠
为锐角，求直线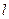的斜率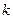
的取值范围
.
（本题12分）
如图，在三棱柱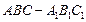
中，已知
，
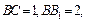
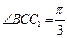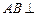侧面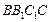
。
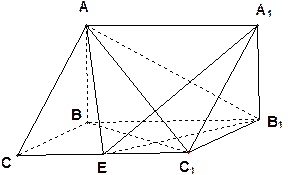
（1）求直线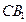
与底面ABC所成角正切值；
（2）在棱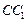
（不包含端点
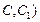上确定一点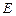
的位置,使得
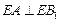(要求说明理由).
（3）在（2）的条件下,若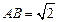
，求二面角
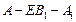的大小.
（本题12分）
有一种舞台灯，外形是正六棱柱，在其每一个侧面
(编号为①②③④⑤⑥)上安装5只颜色各异的灯，假若每只灯正常发光的概率为0.5，若一个侧面上至少有3只灯发光，则不需要更换这个面，否则需要更换这个面，假定更换一个面需要100元，用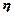
表示更换的面数，用
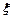表示更换费用。
（1）求①号面需要更换的概率；
（2）求6个面中恰好有2个面需要更换的概率；
（3）写出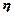的分布列，求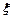的数学期望。
.
