已知函数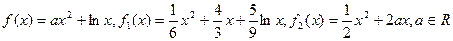 .
.
(1)求函数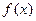 在点
在点 处的切线方程;
处的切线方程;
(2)若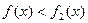 在区间
在区间 上恒成立,求
上恒成立,求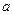 的取值范围;
的取值范围;
(3)当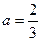 时,求证:在区间
时,求证:在区间 上,满足
上,满足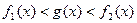 恒成立的函数
恒成立的函数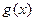 有无穷多个.
有无穷多个.
(本小题满分14分)在三棱锥P-SBC中,A,D分别为边SB,SC的中点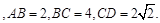 平面PSB
平面PSB 平面ABCD,平面PAD
平面ABCD,平面PAD 平面ABCD
平面ABCD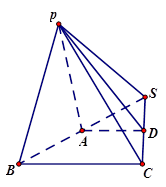
(1)求证:PA⊥BC;
(2)若平面PAD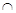 平面PBC=
平面PBC=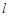 ,求证:
,求证: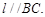
已知向量 ,
,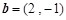 .
.
(1)若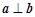 ,求
,求 的值;
的值;
(2)若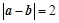 ,
,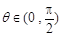 ,求
,求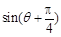 的值
的值
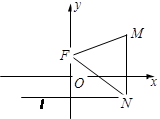
(本小题满分10分)如图,已知点 ,直线
,直线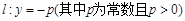 ,
, 为平面内的动点,过
为平面内的动点,过 作
作 的垂线,垂足为
的垂线,垂足为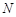 ,且
,且 .
.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)设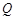 是
是 上的任意一点,过
上的任意一点,过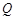 作轨迹
作轨迹 的切线,切点为
的切线,切点为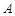 、
、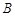 .
.
①求证: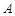 、
、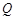 、
、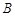 三点的横坐标成等差数列;
三点的横坐标成等差数列;
②若 ,
,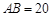 ,求
,求 的值.
的值.
(本小题满分10分)已知数列 满足
满足 ,
,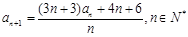 .
.
(1)求证:数列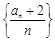 是等比数列;
是等比数列;
(2)设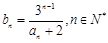 ,求证:当
,求证:当 ,
,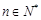 时,
时,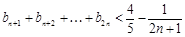 .
.
(选修4-5:不等式选讲)
设 均为正数,
均为正数, .求证:
.求证: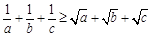 .
.