（本小题满分8分）为了解九年级500名学生平均每天课外阅读的时间，某校随机调查了该年级部分学生一周内平均每天课外阅读的时间（以分钟为单位，并取整数）.现将有关数据整理后绘制成尚未完成的频率分布表和频数分布直方图，请仔细读图完成下列问题：
| 组别 |
分组 |
频数 |
频率 |
| 1 |
14.5—24.5 |
7 |
0.14 |
| 2 |
24.5—34.5 |
a |
0.24 |
| 3 |
34.5—44.5 |
20 |
0. 4 |
| 4 |
44.5—54.5 |
6 |
b |
| 5 |
54.5—64.5 |
5 |
0.1 |
（1）被调查的学生有 名；
（2）频率分布表中，a= ，b= ；
（3）请在题图中补全频数分布直方图；
（4）被调查学生一周内平均每天课外阅读时间的中位数落在第 组；
（5）请估计该年级学生中，大约有 名学生平均每天课外阅读的时间不少于35分钟.
如图1，点P、Q分别是等边△ABC边AB、BC上的动点（端点除外），点P从顶点A、点Q从顶点B同时出发，且它们的运动速度相同，连接AQ、CP交于点M．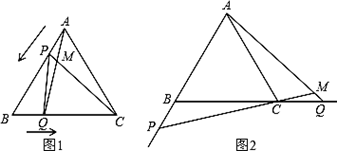
（1）求证：△ABQ≌△CAP；
（2）当点P、Q分别在AB、BC边上运动时，∠QMC变化吗？若变化，请说明理由；若不变，求出它的度数．
（3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠QMC变化吗？若变化，请说明理由；若不变，则求出它的度数．
已知点O到
的两边AB、AC所在直线的距离相等，且OB＝OC．
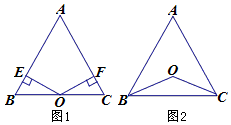
（1）如图1，若点O在边BC上，求证：AB=AC；
（2）如图2，若点O在
的内部，求证：AB=AC；
（3）若点O在的外部，AB=AC成立吗？请画图表示．
某市的A地和B地秋季育苗，急需化肥分别为90吨和60吨，该市的C地和D地分别储存化肥100吨和50吨，全部调配给A地和B地，已知从C、D两地运化肥到A、B两地的运费（元/吨）如下表所示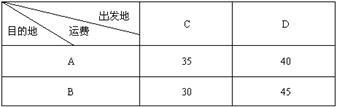
（1）设C地运到A地的化肥为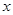
吨，用含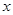（吨）的代数式表示总运费W（元）
（2）求最低总运费，并说明总运费最低时的运送方案
（3）若总运费不少于5680元，共有几种方案？（化肥吨数取整数）
如图，BE⊥AC、CF⊥AB于点E、F，BE与CF交于点D，DE=DF，连接AD．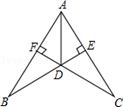
求证：（1）∠FAD=∠EAD；（2）BD=CD．
如图，正方形网格中每一个小正方形的边长都为1，每一个小格的顶点叫做格点．以格点为顶点分别按下列要求画三角形：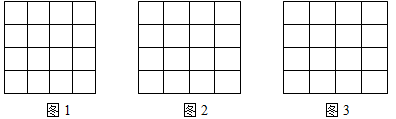
（1）在图1中，画一个三角形，使它的边长都是有理数；
（2）在图2、图3中分别画一个直角三角形，使它们的边长都是无理数，并且要求两个三角形不全等．