(10分)桂林红桥位于桃花江上，是桂林两江四湖的一道亮丽的风景线，该桥的部分横截面
如图所示，上方可看作是一个经过Ａ、Ｃ、Ｂ三点的抛物线，以桥面的水平线为Ｘ轴，经过抛物线的顶点Ｃ与Ｘ轴垂直的直线为Ｙ轴，建立直
角坐标系，已知此桥垂直于桥面的相邻两柱之间距离为２米（图中用线
段ＡＤ、ＣＯ、ＢＥ等表示桥柱）ＣＯ＝１米，ＦＧ＝２米
（１） 求经过Ａ、Ｂ、Ｃ三点的抛物线的解析式。
（２） 求柱子ＡＤ的高度。
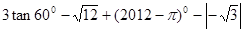
如图，在平面直角坐标系中，抛物线
经过A（3，0），B（0，－3）两点，点P是直线AB上一动点，过点P作
轴的垂线交抛物线于点M，设点P的横坐标为t，分别求直线AB和这条抛物线的解析式
若点P在第四象限，连结BM、AM，当线段PM最长时，求
的面积。
③是否存在这样的点P，使得以点P、M、B、O为顶点的四边形为平行四边形？若存在，请直接写出点P的横坐标；若不存在，请说明理由。
在直角梯形ABCD中，AB∥CD，∠ABC=900，AB=2BC=2CD，对角线AC与BD相交于点O，线段OA、OB的中点分别为点E、F求证：
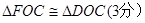
求
的值若直线EF与线段AD、BC分别相交于点G、H，求
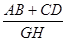的值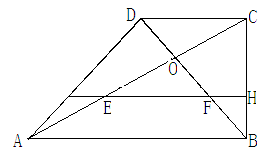
今年春北方严重干旱，某社区人畜饮水紧张，每天需从社区外调运饮用水120吨，有关部门紧急部署，从甲、乙两水厂调运饮用水到社区供水点，甲厂每天最多可调出80吨，乙厂每天最多可调出90吨，从两水厂运水到社区供水点的路程和运费如下表：
| 到社区供水点的路程（千米） |
运费（元/吨·千米） |
|
| 甲厂 |
20 |
12 |
| 乙厂 |
14 |
15 |
若某天调运水的总运费为26700元，则从甲、乙两水厂各调运多少吨饮用水？
设从甲厂调运饮用水
吨，总运费为W元，试写出W关于与的函数关系式，怎样安排调运方案才能使每天的总运费最省？
有3张扑克牌，分别是红桃3，红桃4和黑桃5，把牌洗匀后甲先抽取一张，记下花色和数字后将牌放回，洗匀后乙再抽取一张，先后两次抽得的数字分别记为S和t，求
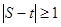的概率甲、乙两人做游戏，现有两种方案：A方案：若两次抽得相同花色则甲胜，否则乙胜，B方案：若两次抽得数字和为奇数则甲胜，否则乙胜；请问甲选择哪种方案胜率较高？