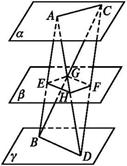
如图所示,两条异面直线AB,CD与三个平行平面α,β,γ分别相交于A,E,B及
C,F,D,又AD、BC与平面β的交点为H,G.
求证：四边形EHFG为平行四边形。
已知椭圆
经过点
,离心率为
．
(1)求椭圆C的方程：
(2)过点Q(1,0)的直线l与椭圆C相交于A、B两点,点P(4,3),记直线PA,PB的斜率分别为k1,k2,当k1·k2最大时,求直线l的方程．
已知函数
．
(1)求
的单调区间；
(2)若
,
在区间
恒成立,求a的取值范围．
在长方体ABCD-A1B1C1D1中,AD＝１,AA1＝AB＝２．点E是线段AB上的动点,点M为D1C的中点．
(1)当E点是AB中点时,求证：直线ME‖平面ADD1 A1；
(2)若二面角AD1ＥＣ的余弦值为
．求线段AE的长．
已知
为等比数列,其中a1=1,且a2,a3+a5,a4成等差数列．
(1)求数列
的通项公式：
(2)设
,求数列{
}的前n项和Tn．
已知函数
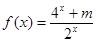是奇函数．
(1)求m的值：
(2)设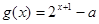
．若函数
与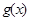
的图象至少有一个公共点．求实数a的取值范围．