某校从参加高一年级期末考试的学生中 抽出60名学生,将其物理成绩(均为整数)分成六段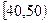 ,
, …
… 后画出如下频率分布直方图.观察图形的信息,回答下列问题:
后画出如下频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)估计这次考试的众数m与中位数n(结果保留一位小数);
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分.
(本小题满分14分)已知函数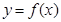 ,
,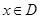 ,设曲线
,设曲线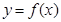 在点
在点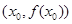 处的切线方程为
处的切线方程为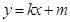 .如果对任意的
.如果对任意的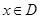 ,均有:
,均有:
①当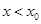 时,
时,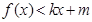 ;
;
②当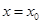 时,
时,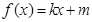 ;
;
③当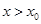 时,
时,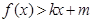 ,
,
则称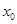 为函数
为函数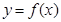 的一个“ʃ-点”.
的一个“ʃ-点”.
(Ⅰ)判断 是否是下列函数的“ʃ-点”:
是否是下列函数的“ʃ-点”:
①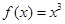 ; ②
; ②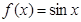 .(只需写出结论)
.(只需写出结论)
(Ⅱ)设函数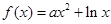 .
.
(ⅰ)若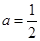 ,证明:
,证明: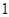 是函数
是函数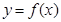 的一个“ʃ-点”;
的一个“ʃ-点”;
(ⅱ)若函数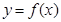 存在“ʃ-点”,直接写出
存在“ʃ-点”,直接写出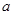 的取值范围.
的取值范围.
(本小题满分13分)已知数列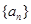 满足
满足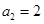 ,
,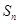 为其前
为其前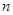 项和,且
项和,且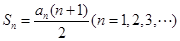 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求证: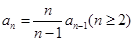 ;
;
(Ⅲ)判断数列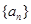 是否为等差数列,并说明理由.
是否为等差数列,并说明理由.
(本小题满分14分)已知函数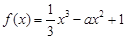 .
.
(Ⅰ)若函数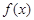 的图象关于点
的图象关于点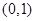 对称,直接写出
对称,直接写出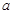 的值;
的值;
(Ⅱ)求函数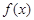 的单调递减区间;
的单调递减区间;
(Ⅲ)若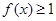 在区间
在区间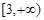 上恒成立,求
上恒成立,求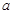 的最大值.
的最大值.
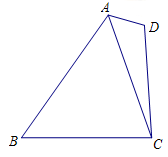
(本小题满分13分)如图所示,在四边形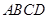 中,
中,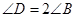 ,且
,且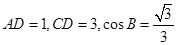 .
.
(Ⅰ)求△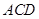 的面积;
的面积;
(Ⅱ)若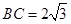 ,求
,求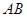 的长.
的长.
(本小题满分13分)设数列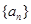 是首项为
是首项为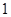 ,公差为
,公差为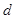 的等差数列,且
的等差数列,且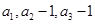 是等比数列
是等比数列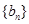 的前三项.
的前三项.
(Ⅰ)求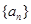 的通项公式;
的通项公式;
(Ⅱ)求数列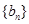 的前
的前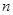 项和
项和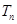 .
.