(本小题满分12分)
已知函数 .
.
(1)求函数 的定义域及
的定义域及 的值;
的值;
(2)判断函数 的奇偶性;
的奇偶性;
(3)判断 在(0,+∞)上的单调性,并给予证明.
在(0,+∞)上的单调性,并给予证明.
(本小题满分12分)某化妆品生产企业为了占有更多的市场份额,拟在2010年世博会期间进行一系列促销活动,经过市场调查和测算,化妆品的年销量x万件与年促销费t万元之间满足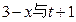 成反比例,如果不搞促销活动,化妆品的年销量只能是1万件,已知2010年生产化妆品的设备折旧、维修等固定费用为3万元,每生产1万件化妆品需要再投入32万元的生产费用,若将每件化妆品的售价定为:其生产成本的150%与平均每件促销费的一半之和,则当年生产的化妆品正好能销完。
成反比例,如果不搞促销活动,化妆品的年销量只能是1万件,已知2010年生产化妆品的设备折旧、维修等固定费用为3万元,每生产1万件化妆品需要再投入32万元的生产费用,若将每件化妆品的售价定为:其生产成本的150%与平均每件促销费的一半之和,则当年生产的化妆品正好能销完。
(1)将2010年利润y(万元)表示为促销费t(万元)的函数;
(2)该企业2010年的促销费投入多少万元时,企业的年利润最大?
(注:利润=销售收入—生产成本—促销费,生产成本=固定费用+生产费用)
(本小题满分12分)
各项均不为零的数列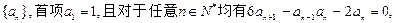
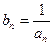
(1)求数列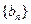 的通项公式;
的通项公式;
(2)数列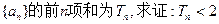
(本小题满分12分)
某项考试按科目A、科目B依次进行 ,只有当科目A成绩合格时,才可以继续参加科目B的考试。每个科目只允许有一次补考机会,两个科目成绩均合格方可获得该项合格证书,现在某同学将要参加这项考试,已知他每次考科目A成绩合格的概率均为
,只有当科目A成绩合格时,才可以继续参加科目B的考试。每个科目只允许有一次补考机会,两个科目成绩均合格方可获得该项合格证书,现在某同学将要参加这项考试,已知他每次考科目A成绩合格的概率均为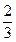 ,每次考科目B成绩合格的概率均为
,每次考科目B成绩合格的概率均为 。假设他在这项考试中不放弃所有的考试机会,且每次的考试成绩互不影响,记他参加考试的次数为X。
。假设他在这项考试中不放弃所有的考试机会,且每次的考试成绩互不影响,记他参加考试的次数为X。
(1)求X的分布列和均值;
(2)求该同学在这项考试中获得合格证书的概率。
如图,四棱锥P—ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB,PA⊥底面ABCD,E是PC的中点。
(1)求证:BE//平面PAD;
(2)若BE⊥平面PCD,①求异面直线PD与BC所成角的余弦值;
②求二面角E—BD—C的余弦值。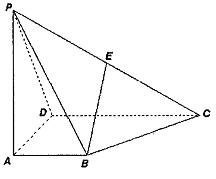
(本小题12分)已知钝角△ABC中,角A、B、C的对边分别为a、b、c,且有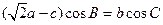
(1)求角B的大小;
(2)
 设向量
设向量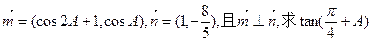 的值。
的值。