已知函数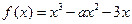
(1)若
在区间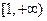
上是增函数，求实数
的取值范围； (2)若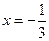
是的极值点，求在
上的最大值；（3）在（2）的条件下，是否存在实数
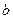，使得函数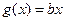
的图像与函数的图象恰有3个交点？若存在，请求出实数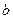的取值范围；若不存在，试说明理由。
已知函数
（1）求函数的周期；
（2）求函数的单调递增区间；
（3）若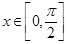
时，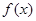
的最小值为– 2 ，求a的值．
在
分别是角A、B、C的对边，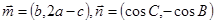
，且
．
（1）求角B的大小；
（2）求sin A＋sin C的取值范围．
已知向量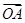
＝(3，－4)，
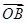＝(6，－3)，
＝(5－m，－3－m)．
（1）若点A，B，C不能构成三角形，求实数m满足的条件；
（2）若△ABC为直角三角形，求实数m的值．
(本小题满分12分)如图，椭圆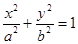
上的点M与椭圆右焦点
的连线
与x轴垂直，且OM（O是坐标原点）与椭圆长轴和短轴端点的连线AB平行．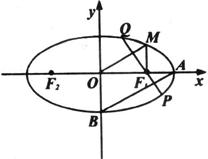
（1）求椭圆的离心率；
（2）过且与AB垂直的直线交椭圆于P、Q，若
的面积是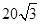
，求此时椭圆的方程．
以下是某地搜集到的新房屋的销售价格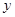
（万元）和房屋的面积
（
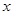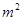）的数据 ，若由资料可知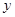对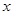呈线性相关关系。
|
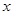80 |
90 |
100 |
110 |
120 |
| y |
48 |
52 |
63 |
72 |
80 |
试求:（1）线性回归方程；
（2）根据（1）的结果估计当房屋面积为
时的销售价格.
参考公式：