已知△ABC中,角A、B、C的对边为a,b,c,向量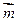
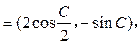
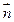 =
=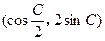 ,且
,且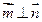 .
.
(1) 求角C;
(2)若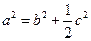 ,试求
,试求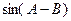 的值.
的值.
某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获最大利润?最大利润有多大?
(1) 已知函数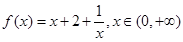 ,求函数
,求函数 的最小值;
的最小值;
(2) 设x,y为正数, 且x+y=1,求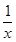 +
+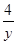 的最小值.
的最小值.
已知{an}为等差数列,且a1+a3=8,a2+a4=12.
(1){an}的通项公式;
(2)记{an}的前n项和为Sn,若a1,ak,Sk+2成等比数列,求正整数k的值.
已知数列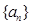 的前
的前 项和
项和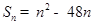 。
。
(1)求数列的通项公式;
(2)求 的最大或最小值。
的最大或最小值。
甲、乙两位学生参加数学竞赛培训。现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据,并指出两组数据的中位数。
(2)从平均数、方差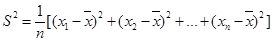 考虑,你认为哪位学生更稳定?请说明理由。
考虑,你认为哪位学生更稳定?请说明理由。