一个均匀的正四面体的四个面上分别涂有1,2,3,4四个数字,现随机投掷两次,正四面体面朝下的数字分别为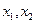 ,记
,记 .
.
(1)分别求出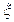 取得最大值和最小值时的概率; (2)
取得最大值和最小值时的概率; (2) 求
求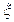 的分布列及数学期望.
的分布列及数学期望.
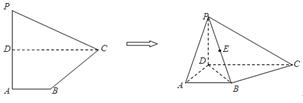
(本小题满分12分)(理科做)如图,已知平面四边形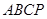 中,
中,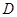 为
为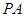 的中点,
的中点,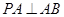 ,
,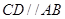 ,且
,且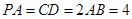 .将此平面四边形
.将此平面四边形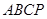 沿
沿 折成直二面角
折成直二面角 ,连接
,连接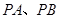 ,设
,设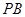 中点为
中点为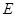 .
.
(1)证明:平面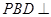 平面
平面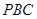 ;
;
(2)在线段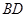 上是否存在一点
上是否存在一点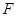 ,使得
,使得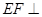 平面
平面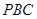 ?若存在,请确定点
?若存在,请确定点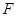 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(3)求直线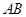 与平面
与平面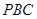 所成角的正弦值.
所成角的正弦值.
(文科做)已知函数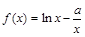 .
.
(1)若a>0,试判断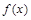 在定义域内的单调性;
在定义域内的单调性;
(2)若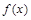 在
在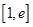 上的最小值为
上的最小值为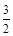 ,求a的值;
,求a的值;
(3)若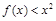 在
在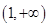 上恒成立,求a的取值范围
上恒成立,求a的取值范围
(本小题共12分)已知在等比数列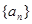 中,
中,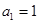 ,且
,且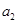 是
是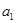 和
和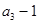 的等差中项.
的等差中项.
(1)求数列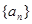 的通项公式;
的通项公式;
(2)若数列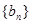 满足
满足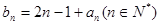 ,求
,求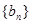 的前
的前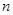 项和
项和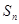 .
.
在△ABC中,a、b、c分别是角A、B、C的对边,且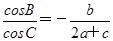 .
.
(1)求角B的大小;
(2)若b=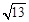 ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.
(本小题满分12分) 已知关于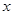 的不等式
的不等式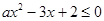 的解集为
的解集为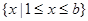 .
.
(1)求实数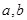 的值;
的值;
(2)解关于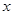 的不等式:
的不等式: (
( 为常数).
为常数).
(本小题满分10分)已知命题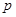 :方程
:方程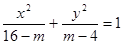 表示焦点在
表示焦点在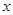 轴上的椭圆;命题
轴上的椭圆;命题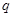 :点
:点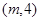 在圆
在圆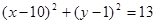 内.若
内.若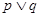 为真命题,
为真命题,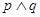 为假命题,试求实数
为假命题,试求实数 的取值范围.
的取值范围.