已知集合

已知函数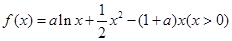 ,其中
,其中 为实数.
为实数.
(1)求函数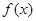 的单调区间;
的单调区间;
(2)若函数 对定义域内的任意
对定义域内的任意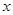 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(3)证明,对于任意的正整数 ,不等式
,不等式 恒成立.
恒成立.
已知 为椭圆
为椭圆 的左右焦点,点
的左右焦点,点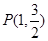 为其上一点,且有
为其上一点,且有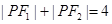
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)过 的直线
的直线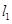 与椭圆
与椭圆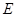 交于
交于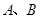 两点,过
两点,过 与
与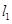 平行的直线
平行的直线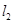 与椭圆
与椭圆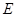 交于
交于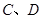 两点,求四边形
两点,求四边形 的面积
的面积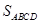 的最大值.
的最大值.
如图,已知四棱锥 的底面为菱形,
的底面为菱形,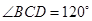 ,
,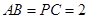 ,
,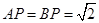 .
.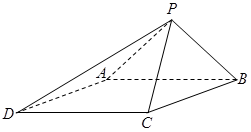
(Ⅰ)求证: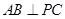 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
某地区2009年至2015年农村居民家庭人均纯收入y(单位:千元)的数据如下表:
| 年份 |
2009 |
2010 |
2011 |
2012 |
2013 |
2014 |
2015 |
| 年份代号t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 人均纯收入y |
2.9 |
3.3 |
3.6 |
4.4 |
4.8 |
5.2 |
5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2009年至2015年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2017年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
在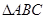 中,角
中,角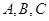 所对的边分别为
所对的边分别为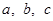 ,满足
,满足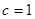 ,且
,且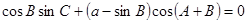 .
.
(1)求角 的大小;
的大小;
(2)求 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角 的值.
的值.