若定义在
上的奇函数
满足当
时，
.
（1）求在上的解析式；
（2）判断在
上的单调性，并给予证明；
（3）当
为何值时，关于方程
在
上有实数解？
已知数列
是公差为正的等差数列,其前
项和为
,点
在抛物线
上；各项都为正数的等比数列
满足
．
（1）求数列，的通项公式；
（2）记
,求数列
的前n项和
．
已知函数
（1）若
求
的值域；
（2）若
为函数
的一个零点，求
的值．
如图，在四棱锥
中，底面
为边长为4的正方形，
平面
，
为
中点， 
．
（1）求证：
．
（2）求三棱锥
的体积．
设数列
、
满足
，
，
，
．
（1）证明：
，
（
）；
（2）设
，求数列
的通项公式；
（3）设数列的前
项和为
，数列的前项和为
，数列
的前项和为
，求证：
．
已知函数
(a为实常数).
(1)若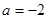
，求证：函数
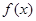在(1，+．∞)上是增函数；
(2)求函数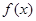在[1，e]上的最小值及相应的
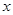值；
(3)若存在
，使得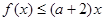
成立，求实数a的取值范围.