（本小题满分12分）已知函数，其中（1）若为偶函数，求a的值-优题课

题文

（本小题满分12分）已知函数
，其中
（1）若为偶函数，求a的值；
（2）命题p：函数上是增函数，命题q：函数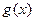是减函数，如果p或q为真，p且q为假，求a的取值范围。
（3）在（2）的条件下，比较的大小。

科目数学题型解答题难度较难

相关试题

在锐角 $∆ A B C$ 中,内角 $A, B, C$ 的对边分别为 $a, b, c$ ,且 $2 a \sin B = \sqrt{3} b$ ．
(Ⅰ)求角A的大小；
(Ⅱ)若 $a = 6, b + c = 8$ ,求 $∆ A B C$ 的面积．

已知函数 $f (x) = e^{x}, x \in R$ .
（1）求 $f (x)$ 的反函数的图象上图象上，点(1,0)处的切线方程;
（2）证明: 曲线 $y = f (x)$ 与曲线 $y = \frac{1}{2} x^{2} + x + 1$ 有唯一公共点.
（3）设 $a < b$ , 比较 $f (\frac{a + b}{2})$ 与 $\frac{f (b) - f (a)}{b - a}$ 的大小, 并说明理由.

已知动点 $M (x, y)$ 到直线 $l : x = 4$ 的距离是它到点 $N (1, 0)$ 的距离的2倍.
（1）求动点 $M$ 的轨迹 $C$ 的方程;
（2）过点 $P (0, 3)$ 的直线 $m$ 与轨迹 $C$ 交于 $A, B$ 两点.若 $A$ 是 $P B$ 的中点,求直线 $m$ 的斜率.

有7位歌手(1至7号)参加一场歌唱比赛, 由500名大众评委现场投票决定歌手名次, 根据年龄将大众评委分为5组, 各组的人数如下:

组别	A	B	C	D	E
人数	50	100	150	150	50

（1）为了调查评委对7位歌手的支持状况, 现用分层抽样方法从各组中抽取若干评委, 其中从B组中抽取了6人. 请将其余各组抽取的人数填入下表.

组别	A	B	C	D	E
人数	50	100	150	150	50
抽取人数		6

（2）在（1）中, 若A, B两组被抽到的评委中各有2人支持1号歌手, 现从这两组被抽到的评委中分别任选1人, 求这2人都支持1号歌手的概率.

如图,四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的底面 $A B C D$ 是正方形, $O$ 为底面中心, $A_{1} O ⊥$ 平面 $A B C D$ , $A B = A A_{1} = \sqrt{2}$ .

（1）证明: $A_{1} B D / /$ 平面 $C D_{1} B_{1}$ ;
（2）求三棱柱 $A B D - A_{1} B_{1} D_{1}$ 的体积.

试卷网试题网古诗词网作文网范文网