(本小题满分l2分)
已知命题p:“∀x∈[1,2],x2-a≥0”,命题q:“∃x0∈R,
x+2ax0+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围.
在平面直角坐标系内,动圆 过定点
过定点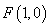 ,且与定直线
,且与定直线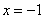 相切.
相切.
(1)求动圆圆心 的轨迹
的轨迹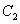 的方程;
的方程;
(2)中心在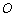 的椭圆
的椭圆 的一个焦点为
的一个焦点为 ,直线过点
,直线过点 .若坐标原点
.若坐标原点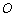 关于直线的对称点
关于直线的对称点 在曲线
在曲线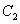 上,且直线与椭圆
上,且直线与椭圆 有公共点,求椭圆
有公共点,求椭圆 的长轴长取得最小值时的椭圆方程.
的长轴长取得最小值时的椭圆方程.
如图甲,设正方形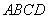 的边长为
的边长为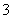 ,点
,点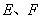 分别在
分别在 上,并且满足
上,并且满足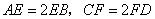 ,如图乙,将直角梯形
,如图乙,将直角梯形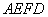 沿
沿 折到
折到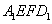 的位置,使点
的位置,使点 在
在
平面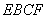 上的射影
上的射影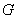 恰好在
恰好在 上.
上.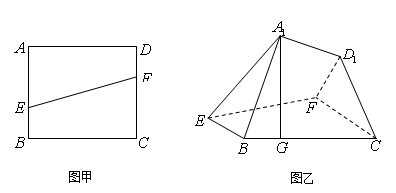
(1)证明: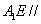 平面
平面 ;
;
(2)求平面 与平面
与平面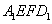 所成二面角的余弦值.
所成二面角的余弦值.
市民李生居住在甲地,工作在乙地,他的小孩就读的小学在丙地,三地之间的道路情
况如图所示.假设工作日不走其它道路,只在图示的道路中往返,每次在路口选择道路是随机
的.同一条道路去程与回程是否堵车相互独立. 假设李生早上需要先开车送小孩去丙地小学,
再返回经甲地赶去乙地上班.假设道路 、
、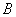 、
、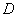 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是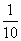 ,
,
道路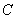 、
、 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是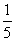 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.
(1)求李生小孩按时到校的概率;
(2)李生是否有八成把握能够按时上班?
(3)设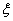 表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求
表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求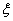 的均值.
的均值.
在平面直角坐标系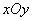 中,以
中,以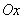 为始边,角
为始边,角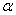 的终边与单位圆
的终边与单位圆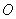 的交点
的交点 在
在
第一象限,已知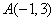 .
.
(1)若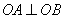 ,求
,求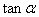 的值;
的值;
(2)若 点横坐标为
点横坐标为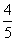 ,求
,求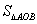 .
.
已知数列{ }的前
}的前 项和为
项和为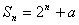 (
( 为常数,
为常数, N*).
N*).
(1)求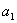 ,
,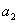 ,
,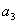 ;
;
(2)若数列{ }为等比数列,求常数
}为等比数列,求常数 的值及
的值及 ;
;
(3)对于(2)中的 ,记
,记 ,若
,若 对任意的正整数
对任意的正整数 恒成立,求实数
恒成立,求实数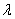 的取值范围.
的取值范围.