一名足球守门员练习折返跑，从球门线出发，向前记作正数，返回记作负数，他的记录如下：（单位：米）＋5，-3，＋10，-8，-6，＋12，-10.
（1）守门员最后是否回到了球门线的位置？
（2）守门员全部练习结束后，他共跑了多少米？
（3）在练习过程中，守门员离开球门线最远距离是多少米？（此小题只写出答案）
建立两个适当的平面直角坐标系，分别表示边长为8的正方形的顶点的坐标
如果│3x+3│+│x+3y－2│＝0，那么点P(x，y)在第几象限?点Q(x+1，y－1)在坐标平面内的什么位置?
王霞和爸爸、妈妈到人民公园游玩，回到家后，她利用平面直角坐标系画出了公园的景区地图，如图所示。可是她忘记了在图中标出原点和x轴、y轴。只知道游乐
园D的坐标为（2，－2），你能帮她求出其他各景点的坐标？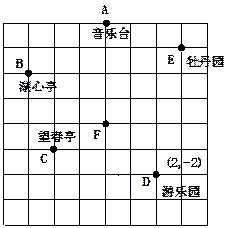
已知点A（-2，0）B（4，0）C（-2，-3）。
（1）求A、B两点之间的距离。
（2）求点C到X轴的距离。
（3）求△ABC的面积
设M（a,b）为平面直角坐标系中的点
(1 )当a﹥0,b﹤0时，点M位于第几象限？
﹙2﹚当ab﹥0时，点M位于第几象限？
﹙3﹚当a为任意实数，且b﹤0时，点M位于何处？