规定一种新的运算:A★B = A×B−A−B+1,如3★4 =" 3×4−3−4+1" = 6.
请比较(−3)★4与2★(−5)的大小。
两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O为边AC和DF的交点,不重叠的两部分△AOF与△DOC是否全等?为什么?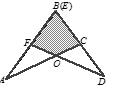
解不等式组: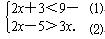
解方程: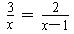 .
.
已知抛物线的顶点是C (0,a) (a>0,a为常数),并经过点(2a,2a),点D(0,2a)为一定点.
(1)求含有常数a的抛物线的解析式;
(2)设点P是抛物线任意一点,过P作PH⊥x轴,垂足是H,求证:PD = PH;
(3)设过原点O的直线l与抛物线在第一象限相交于A、B两点,若DA=2DB,且S△ABD =  ,求a的值.
,求a的值.
已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧 上取一点E使∠EBC = ∠DEC,延长BE依次交AC于G,交⊙O于H.
上取一点E使∠EBC = ∠DEC,延长BE依次交AC于G,交⊙O于H.
(1)求证:AC⊥BH
(2)若∠ABC= 45°,⊙O的直径等于10,BD =8,求CE的长.
 |