图1是由若干个小圆圈堆成的一个形如正三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了n层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为：1+2+3+…+n=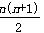 
图１ 图2 图3 图4
如果图1中的圆圈共有12层，
（1）我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数1， 2，3，4…，则最底层最左边这个圆圈中的数是 ；
（2）我们自上往下，在每个圆圈中都按图4的方式填上一串连续的整数−40，−39，−38，…，求图4中所有圆圈中各数的和．
如图，BD为⊙O的直径，AB=AC，AD交BC于点E，AE=2，ED=4．
（1）判断△ABE与△ADB是否相似，并说明理由；
（2）求AB的长。
（3）求
的正切值；
已知二次函数
的图象C1与x轴有且只有一个公共点．
（1）求C1的顶点坐标；
（2）将C1向下平移若干个单位后，得抛物线C2，如果C2与x轴的一个交点为A（—3，0），求C2的函数关系式，并求C2与x轴的另一个交点坐标；
在Rt△ABC中，∠C＝900， tanB=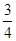
， ∠ADC=45°，DC=6，求sin∠BAD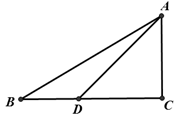
如图，△ABC中，CD是边AB上的高，且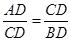
．
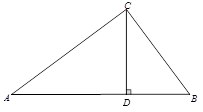
（1）求证△ACD∽△CBD；
（2）求∠ACB的大小．
已知：关于x的一元二次方程x2—（m—1）x＋m＋2＝0
（1）若方程有两个相等的实数根，求m的值；
（2）若Rt△ABC中，∠C＝90°，tanA的值恰为（1）中方程的根，求cosB的值．