(本题12分) 如图,在平行四边形ABCD中,AB在x轴上,D点y轴上, ,
, ,B点坐标为(4,0).点
,B点坐标为(4,0).点 是边
是边 上一点,且
上一点,且 .点
.点 、
、 分别从
分别从 、
、 同时出发,以1厘米/秒的速度分别沿
同时出发,以1厘米/秒的速度分别沿 、
、 向点
向点 运动(当点F运动到点B时,点E随之停止运动),EM、CD的延长线交于点P,FP交AD于点Q.⊙E半径为
运动(当点F运动到点B时,点E随之停止运动),EM、CD的延长线交于点P,FP交AD于点Q.⊙E半径为 ,设运动时间为
,设运动时间为 秒。
秒。
(1)求直线BC的解析式。
(2)当 为何值时,
为何值时, ?
?
(3)在(2)问条件下,⊙E与直线PF是否相切;如果相切,加以证明,并求出切点的坐标。如果不相切,说明理由。
(.重庆市B卷,第20题,7分)如图,△ABC和△EFD分别在线段AE的两侧,点C,D在线段AE上,AC=DE,AB=EF,AB∥EF.
求证:BC=FD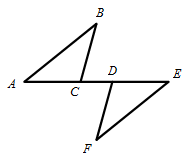
(.重庆市A卷,第25题,12分)如图1,在△ABC中,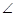 ACB=90°,
ACB=90°,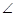 BAC=60°,点E是∠BAC角平分线上一点,过点E作AE的垂线,过点A作AB的线段,两垂线交于点D,连接DB,点F是BD的中点.DH⊥AC,垂足为H,连接EF,HF。
BAC=60°,点E是∠BAC角平分线上一点,过点E作AE的垂线,过点A作AB的线段,两垂线交于点D,连接DB,点F是BD的中点.DH⊥AC,垂足为H,连接EF,HF。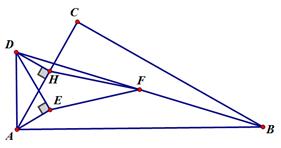
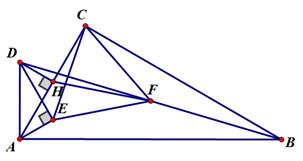
2图1图2
(1)如图1,若点H是AC的中点,AC=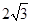 ,求AB,BD的长。
,求AB,BD的长。
(2)如图1,求证:HF=EF。
(3)如图2,连接CF,CE,猜想:△CEF是否是等边三角形?若是,请证明;若不是,请说明理由。
(.重庆市A卷,第20题,7分)如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,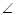 B=
B=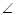 E。
E。
求证: ADB=
ADB=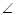 FCE.
FCE.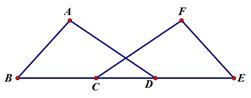
(.河南省,第20题,9分)如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30º,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,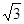 ≈1.73)
≈1.73)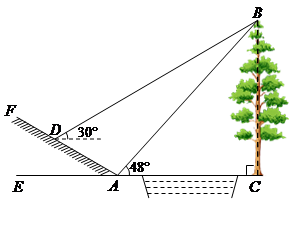
(.陕西省,第12题,3分)请从以下两小题中任选一个作答,若多选,则按第一题计分。
A.正八边形一个内角的度数为______________。
B.如图,有一滑梯AB,其水平宽度AC为5.3米,铅直高度BC为2.8米,则∠A的度数约为__________。(用科学计算器计算,结果精确到0.1°)