(本题10分)
(1)拼一拼,画一画:请你用4个长为a,宽为b的矩形拼成一个大正方形,并且正中间留下一个洞,这个洞恰好是一个小正方形。
(2)用不同方法计算中间的小正方形的面积,聪明的你能发现什么?
(3)当拼成的这个大正方形边长比中间小正方形边长多3cm时,它的面积就多24cm2,求中间小正方形的边长。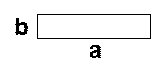
某市在道路改造过程中,需要铺设一条长为1000米的管道,决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米,且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.甲、乙工程队每天各能铺设多少米?
如果要求完成该项工程的工期不超过10天,那么为两工程队分配工程量(以百米为单位)的方案有几种?请你帮助设计出来.
如图已知函数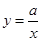 的图象与直线
的图象与直线 相交于点A(1,3)、B(
相交于点A(1,3)、B( ,1)两点,
,1)两点,求
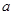 、
、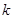 、
、 的值;
的值;写出不等式
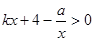 的解集(请直接写出答案);
的解集(请直接写出答案);根据图像写出:使反比例函数的值大于-3时x的取值范围。
当x取什么范围时,y=kx+4的值满足-2≤y<1。
求△AOB的面积。

在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上。填空:∠ABC=°,BC=.
判断△ABC与△DEF是否相似,并说明理由.

一天,小明和小玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式。比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.图③可以解释为等式:
在虚线框中用图①中的基本图形拼成若干块(每种至少用一次)拼成一个矩形,使拼出的矩形面积为2a2+7ab+3b2,并标出此矩形的长和宽.
如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下关系式
(1)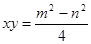 (2)
(2)
(3)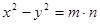 (4)
(4)
其中正确的有几个………………………………()
| A.1个 | B.2个 | C.3个 | D.4个 |

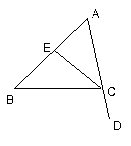
已知:如图,在△ABC中,∠B=40°,∠BCD=100°,EC平分∠ACB,
求:∠A与∠ACE的度数.