某商品每件成本9元,售价为30元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值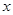 (单位:元,
(单位:元,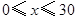 )的平方成正比,已知商品单价降低2元时,一星期多卖出24件.
)的平方成正比,已知商品单价降低2元时,一星期多卖出24件.
(I)将一个星期的商品销售利润表示成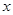 的函数;
的函数;
(II)如何定价才能使一个星期的商品销售利润最大?
数列{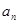 }满足
}满足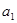 =1,
=1, =
=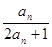 ,(1)计算
,(1)计算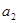 ,
, ,
,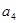 的值;
的值;
(2)归纳推测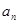 ,并用数学归纳法证明你的推测.
,并用数学归纳法证明你的推测.
已知函数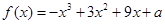
(1)求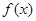 的单调递减区间;
的单调递减区间;
(2)若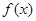 在区间
在区间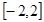 上的最大值为20,求它在该区间上的最小值。
上的最大值为20,求它在该区间上的最小值。
从4名男生,3名女生中选出三名代表:
(1)不同的选法共有多少种?
(2)至少有一名女生的不同的选法共有多少种?
(3)代表中男、女生都要有的不同的选法共有多少种?
已知函数 ,
,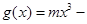
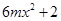
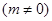 ,
, 在
在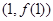 处的切线方程为
处的切线方程为 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)是否总存在实数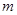 ,使得对任意的
,使得对任意的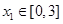 ,总存在
,总存在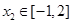 ,使得
,使得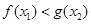 成立?若存在,求出实数
成立?若存在,求出实数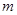 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.