某企业拟建造如图所示的容器（不计厚度，长度单位：米），其中容器的中间为圆柱形，左右两端均为半球形，按照设计要求容器的体积为
立方米，且
．假设该容器的建造费用仅与其表面积有关．已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为
千元．设该容器的建造费用为
千元．
（1）写出
关于
的函数表达式，并求该函数的定义域；
（2）求该容器的建造费用最小时的
．
在
中，a、b、c分别是角A、B、C的对边，且
为最大边，
.
（1）求
的值；
（2）若
，求边长.
已知等比数列
前
项之和为
，
，
，求
和
（本小题满分12分）
有一个容量为50的样本，数据的 分组及各组的频数如下
3;
8；
9；
11；
10；
5；
4.
（1）列频率分布表
（2）画出频率分布直方图
（3）根据频率分布直方图估计数据落在
的概率是多少
（本小题满分12分）
假
设你家订了一份报纸，送报人可能在早上6点—8点之间把报纸送到你家，你每天离家去工作的时间在早上7点—9点之间 ，求你离家前不能看到报纸（称事件A）的概率是多少？
本小题满分12分）
某
次运动会甲、乙两名射击运动员成绩如下：
甲：9.4，8.7，7.5，8.4，10.1，10.5，10.7，7.2，7.8，10.8；
乙：9.1，8.7，7.1，9.8，9.7，8.
5，1
0.1，9.2，10.1，9.1；
（1）用茎叶图表示甲，乙两个成绩；
（2）分别计算两个样本的平均数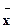
和标准差s，并根据计算结果估计哪位运动员的成绩比较稳定。