如图,多边形ABCDE中,∠ABC=90°,AD∥BC,△ADE是正三角形,AD=2,AB=BC=1,沿直线AD将△ADE折起至△ADP的位置,连接PB,BC,构成四棱锥P-ABCD,使得∠PAB=90°.点O为线段AD的中点,连接PO.

(1)求证:PO⊥平面ABCD;
(2)求异面直线CD与PA所成角的余弦值.
设关于x的一元二次方程x2+2ax+b2=0
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]任取的一个实数,b是从区间[0,2]任取的一个实数,求上述方程有实根的概率.
已知点P(x1,y1),Q(x2,y2)是函数f(x)=sin(ωx+Φ)(ω>0,0<Φ< )图象上的任意两点,若|y1-y2|=2时,|x1-x2|的最小值为
)图象上的任意两点,若|y1-y2|=2时,|x1-x2|的最小值为 ,且函数f(x)的图象经过点(0,2),在△ABC中,角A,B,C的对边分别为a,b,c,且2sinAsinC+cos2B=1.
,且函数f(x)的图象经过点(0,2),在△ABC中,角A,B,C的对边分别为a,b,c,且2sinAsinC+cos2B=1.
(1)求函数f(x)的解析式;
(2)求g(B)= f(B)+f(B+
f(B)+f(B+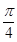 )的取值范围.
)的取值范围.
(本小题满分14分)设函数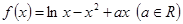 .
.
(1)求函数 的单调区间;
的单调区间;
(2)已知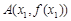 ,
,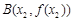 (
( )是函数
)是函数 在
在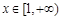 的图象上的任意两点,且满足
的图象上的任意两点,且满足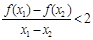 ,求a的最大值;
,求a的最大值;
(3)设 ,若对于任意给定的
,若对于任意给定的 ,方程
,方程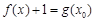 在
在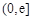 内有两个不同的实数根,求a的取值范围.(其中
内有两个不同的实数根,求a的取值范围.(其中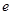 是自然对数的底数)
是自然对数的底数)
(本小题满分13分)已知数列 的前n项和为
的前n项和为 ,
, (
( ),
), .
.
(1)当t为何值时,数列 是等比数列?
是等比数列?
(2)设数列 的前n项和为
的前n项和为 ,
,  ,点
,点 在直线
在直线 上,在(1)的条件下,若不等式
上,在(1)的条件下,若不等式 对于
对于 恒成立,求实数m的最大值.
恒成立,求实数m的最大值.