如图,在四棱锥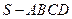 中,底面
中,底面 为正方形,侧棱
为正方形,侧棱
 底面
底面 ,
,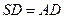 ,
,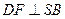 垂足为
垂足为 ,
, 是
是 的中点.
的中点.
( Ⅰ)证明:
Ⅰ)证明: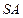 ∥平面
∥平面 ;
;
(Ⅱ)证明:平面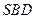 ⊥平面
⊥平面 .
.
已知向量 (
( 为常数且
为常数且 ),函数
),函数 在
在 上的最大值为
上的最大值为 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)把函数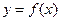 的图象向右平移
的图象向右平移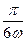 个单位,可得函数
个单位,可得函数 的图象,若
的图象,若 在
在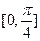 上为增函数,求
上为增函数,求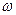 的最大值.
的最大值.
(本小题满分14分)如图, 为等腰直角
为等腰直角 的直角顶点,
的直角顶点,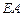 、
、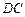 都垂直于
都垂直于 所在的平面,
所在的平面,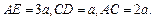

(1)求二面角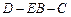 的大小;
的大小;
(2)求点 到平面
到平面 的距离;
的距离;
(3)问线段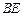 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 且
且 若存在,请指出
若存在,请指出 点的位置;若不存在,请说明理由.
点的位置;若不存在,请说明理由.
(本小题满分13分)如图,在梯形 中,
中,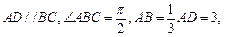


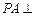 平面
平面 ,且
,且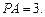
(1)求异面直线 与
与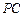 间的距离;
间的距离;
(2)求直线 与平面
与平面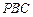 所成的角;
所成的角;
(3)已知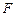 是线段
是线段 上的动点,若二面角
上的动点,若二面角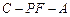 的
的
大小为 ,求AF.
,求AF.
(本小题满分12分)号码为1、2、3、4、5、6的六个大小相同的球,放入编号为1、2、3、4、5、6的六个盒子中,每个盒子只能放一个球.
(1)若1、2号球要放入号码是相邻数字的两个盒子中,则不同的放法有多少种?
(2)若3、4号球要放入编号不比自己号码小的盒子中,则不同的放法有多少种?
(3)若1号球不放入1号盒中,6号球不放入6号盒中,则不同的放法有多少种?
(本小题满分12分)如图,四边形 是边长为
是边长为 的正方形,
的正方形,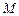 、
、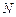 分别是边
分别是边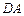 、
、 上的点(M不与A、D重合),且
上的点(M不与A、D重合),且 ,
, 交
交 于点
于点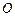 ,沿
,沿 将正方形折成直二面角
将正方形折成直二面角
(1)当 平行移动时,
平行移动时, 的大小是否发生变化?试说明理由;
的大小是否发生变化?试说明理由;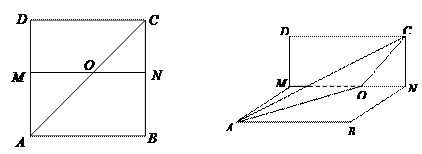 (2)当
(2)当 在怎样的位置时,
在怎样的位置时, 、
、 两点间的距离最小?并求出这个最小值.
两点间的距离最小?并求出这个最小值.