(本小题满分12分)
求下列各圆的标准方程:
(1)圆心在 上且过两点(2,0),(0,-4)
上且过两点(2,0),(0,-4)
(2)圆心在直线 上,且与直线
上,且与直线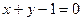 切于点(2,-1)
切于点(2,-1)
等比数列{an}的各项均为正数,且2a1+3a2=1,a32=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列 的前n项和.
的前n项和.
对于函数 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式 对定义域中的每一个
对定义域中的每一个 都成立,则称函数
都成立,则称函数 是“(
是“( )型函数”.
)型函数”.
(1) 判断函数 是否为“(
是否为“( )型函数”,并说明理由;
)型函数”,并说明理由;
(2) 若函数 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对 ;
;
(3)已知函数 是“(
是“( )型函数”,对应的实数对
)型函数”,对应的实数对 为(1,4).当
为(1,4).当 时,
时,

 ,若当
,若当 时,都有
时,都有 ,试求
,试求 的取值范围.
的取值范围.
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当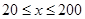 时,车流速度
时,车流速度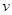 是车流密度x的一次函数.
是车流密度x的一次函数.
(1)当 时,求函数
时,求函数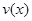 的表达式;
的表达式;
(2)当车流密度 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时)
可以达到最大,并求出最大值(精确到1辆/小时)
已知函数
(1)用定义证明 在
在 上单调递增;
上单调递增;
(2)若 是
是 上的奇函数,求
上的奇函数,求 的值;
的值;
(3)若 的值域为D,且
的值域为D,且 ,求
,求 的取值范围
的取值范围
已知函数 .
.
(1)请在所给的平面直角坐标系中画出函数 的图像;
的图像;
(2)根据函数 的图像回答下列问题:
的图像回答下列问题:
①求函数 的单调区间;
的单调区间;
②求函数 的值域;
的值域;
③求关于 的方程
的方程 在区间
在区间 上解的个数.
上解的个数.
(回答上述3个小题都只需直接写出结果,不需给出演算步骤)