(本小题12分)
如图,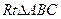 中,
中,
 ,
, .它的顶点
.它的顶点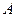 的坐标为
的坐标为 ,顶点
,顶点 的坐标为
的坐标为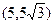 ,点
,点 从点
从点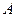 出发,沿
出发,沿 的方向匀速运动,同时点
的方向匀速运动,同时点 从点
从点 出发,沿
出发,沿 轴正方向以相同速度运动,当点
轴正方向以相同速度运动,当点 到达点
到达点 时,两点同时停止运动,设运动的时间为
时,两点同时停止运动,设运动的时间为 秒.
秒.
(1)求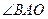 的度数.(直接写出结果)
的度数.(直接写出结果)
(2)当点 在
在 上运动时,
上运动时,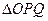 的面积
的面积 与时间
与时间 (秒)之间的函数图象为抛物线的一部分(如图),求点
(秒)之间的函数图象为抛物线的一部分(如图),求点 的运动速度.
的运动速度.
(3)求题(2)中面积 与时间
与时间 之间的函数关系式,及面积
之间的函数关系式,及面积 取最大值时点
取最大值时点 的坐标.
的坐标.
(4)如果点 保持题(2)中的速度不变,当t取何值时,PO=PQ,请说明理由.
保持题(2)中的速度不变,当t取何值时,PO=PQ,请说明理由.
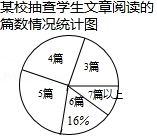
我市自开展“学习新思想,做好接班人”主题阅读活动以来,受到各校的广泛关注和同学们的积极响应,某校为了解全校学生主题阅读的情况,随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表
|
文章阅读的篇数(篇 |
3 |
4 |
5 |
6 |
7及以上 |
|
人数(人 |
20 |
28 |
|
16 |
12 |
请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和 的值;
(2)求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有800名学生,根据抽查结果,估计该校学生在这一周内文章阅读的篇数为4篇的人数.
已知抛物线 与 轴有两个不同的交点.
(1)求 的取值范围;
(2)若抛物线 经过点 和点 ,试比较 与 的大小,并说明理由.
化简: .
计算: .
如图,已知锐角三角形 内接于圆 , 于点 ,连接 .
(1)若 ,
①求证: .
②当 时,求 面积的最大值.
(2)点 在线段 上, ,连接 ,设 , , 是正数),若 ,求证: .
