为了提高产品的年产量,某企业拟在2010年进行技术改革.经调查测算,产品当年的产量x万件与投入技术改革费用m万元(m≥0)满足x=3-(k为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产的产品均能销售出去.厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金).
(1)将2010年该产品的利润y万元(利润=销售金额-生产成本-技术改革费用)表示为技术改革费用m万元的函数;
(2)该企业2010年的技术改革费用投入多少万元时,厂家的利润最大?
已知数列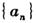 的前n项和
的前n项和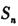 满足
满足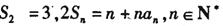 .
.
(2) 求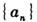 的通项公式,并求数列
的通项公式,并求数列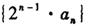 的前n项和
的前n项和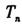 ;
;
(3)设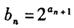 ,证明:
,证明: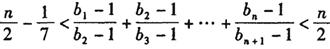
高三年级在综合素质评价的某个维度的测评中,依据评分细则,学生之间相互打分,最终将所有的数据合成一个分数,满分100分.按照大于等于80分为优秀,小于80分为合格.为了解学生在该维度的测评结果,从毕业班中随机抽出一个班的数据.该班共有60名学生,得到如下的列联表.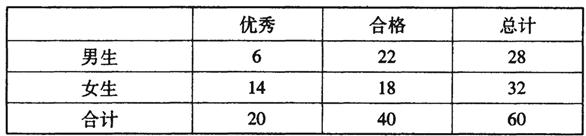
(2) 能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系?
(3) 如果想了解全年级学生该维度的表现情况,采取简单随机抽样的方式在全校学生中抽取少数一部分人来分析,请你选择一个合适的抽样方法,并解释理由;
(4) 学生代表、教师代表、家长代表、教务员四人,分别对测评结果是优秀的20名学生进行检查,检查他们是否躲优秀的相4名检查人员各自纖立的舰20学生中随机抽取一名,设其中男生的人数为随机变量x,求随机变量x的分布列期望.
已知椭圆C: 的左、右焦点分别为F1 ,F2,若椭圆上总存在点P,使得点P在以F1,F2为直径的圆上.
的左、右焦点分别为F1 ,F2,若椭圆上总存在点P,使得点P在以F1,F2为直径的圆上.
(1) 求椭圆离心率的取值范围;
(2) 若AB是椭圆C的任意一条不垂直x轴的弦,M为弦的中点,且满足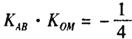 (其中
(其中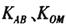 分别表示直线AB、OM的斜率,0为坐标原点),求满足题意的椭圆C的方程.
分别表示直线AB、OM的斜率,0为坐标原点),求满足题意的椭圆C的方程.
如图,四边形ABCD为正方形,四边形BDEF为矩形,AB=2BFiDE丄平面ABCD,G为EF中点.
(1)求证:CF//平面
(2)求证:平面ASG丄平面CDG;
(3)求二面角C—FG—B的余弦值.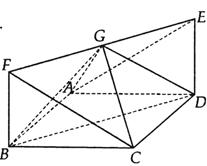
将函数 的图像上各点的横坐标缩短为原来的
的图像上各点的横坐标缩短为原来的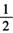 (纵坐标不变),再向左平移
(纵坐标不变),再向左平移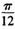 个单位后,得到的图像与函数g(x)=sin 2x的图像重合.
个单位后,得到的图像与函数g(x)=sin 2x的图像重合.
(1)写出函数y=f(x)的图像的一条对称轴方程;
(2)若A为三角形的内角,且 •,求
•,求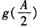 的值
的值