已知动点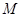 到点
到点 的距离,等于它到直线
的距离,等于它到直线 的距离.
的距离.
(1)求点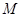 的轨迹
的轨迹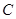 的方程;
的方程;
(2)过点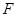 任意作互相垂直的两条直线
任意作互相垂直的两条直线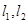 ,分别交曲线
,分别交曲线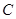 于点
于点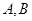 和
和 .
.
设线段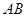 ,
,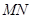 的中点分别为
的中点分别为 ,求证:直线
,求证:直线 恒过一个定点;
恒过一个定点;
(3)在(2)的条件下,求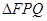 面积的最小值
面积的最小值
已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.
(1)证明: 平面
平面 ;
;
(2)求二面角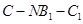 的余弦值;
的余弦值;
(3)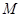 为
为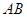 的中点,在线段
的中点,在线段 上是否存在一点
上是否存在一点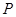 ,使得
,使得 平面
平面 ,若存在,求出
,若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
某商场“五一”期间举行有奖促销活动,顾客只要在商店购物满800元就能得到一次摸奖机会.摸奖规则是:在盒子内预先放有5个大小相同的球,其中一个球标号是0,两个球标号都是40,还有两个球没有标号。顾客依次从盒子里摸球,每次摸一个球(不放回),若累计摸到两个没有标号的球就停止摸球,否则将盒子内球摸完才停止.奖金数为摸出球的标号之和(单位:元),已知某顾客得到一次摸奖机会。
(1)求该顾客摸三次球被停止的概率;
(2)设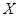 为该顾客摸球停止时所得的奖金数,求
为该顾客摸球停止时所得的奖金数,求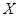 的分布列及均值.
的分布列及均值.
在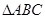 中,角
中,角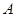 、
、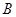 、
、 的对边分别为
的对边分别为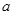 、
、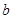 、
、 .已知
.已知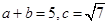 ,且
,且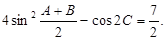
(1) 求角 的大小;
的大小;
(2)求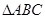 的面积
的面积
等比数列{an}的各项均为正数,且 。
。
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前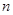 项和.
项和.