已知动点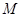 到点
到点 的距离,等于它到直线
的距离,等于它到直线 的距离.
的距离.
(1)求点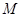 的轨迹
的轨迹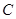 的方程;
的方程;
(2)过点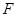 任意作互相垂直的两条直线
任意作互相垂直的两条直线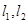 ,分别交曲线
,分别交曲线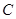 于点
于点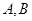 和
和 .
.
设线段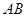 ,
,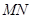 的中点分别为
的中点分别为 ,求证:直线
,求证:直线 恒过一个定点;
恒过一个定点;
(3)在(2)的条件下,求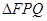 面积的最小值
面积的最小值
(本小题满分10分 )选修4—1:几何证明选讲
如图, 为⊙
为⊙ 的直径,直线
的直径,直线 与⊙
与⊙ 相切于点
相切于点 ,
, 垂直
垂直 于点
于点 ,
, 垂直
垂直 于点
于点 ,
, 垂直
垂直 于点
于点 ,连接
,连接 ,
, .
.
证明:(Ⅰ) ;
;
(Ⅱ) .
.
(本小题满分12分)已知函数 .
.
(I)讨论函数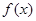 的单调区间;
的单调区间;
(II)当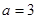 时,若函数
时,若函数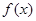 在区间
在区间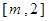 上的最大值为
上的最大值为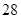 ,求
,求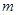 的取值范围.
的取值范围.
(本小题满分12分)在平面直角坐标系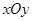 中,已知圆心在
中,已知圆心在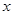 轴上,半径为4的圆
轴上,半径为4的圆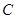 位于
位于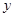 轴右侧,且与
轴右侧,且与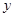 轴相切.
轴相切.
(I)求圆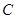 的方程;
的方程;
(II)若椭圆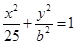 的离心率为
的离心率为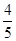 ,且左右焦点为
,且左右焦点为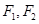 .试探究在圆
.试探究在圆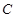 上是否存在点
上是否存在点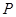 ,使得
,使得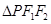 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
(本小题满分12分)如图,矩形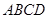 中,对角线
中,对角线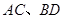 的交点为
的交点为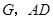 ⊥平面
⊥平面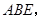
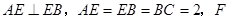 为
为 上的点,且
上的点,且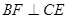 .
.
(I)求证: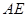 ⊥平面
⊥平面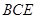 ;
;
(II)求三棱锥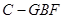 的体积.
的体积.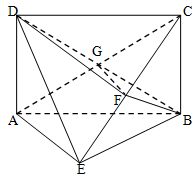
(本小题满分12分)某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.
(I)计算甲班7位学生成绩的方差 ;
;
(II)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.
参考公式:
方差 ,其中
,其中 .
.