(本小题满分12分)某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.
(I)计算甲班7位学生成绩的方差 ;
;
(II)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.
参考公式:
方差 ,其中
,其中 .
.
已知 为等差数列,
为等差数列,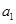 +
+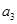 +
+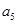 =105,
=105,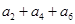 =99,
=99,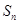 表示
表示 的前
的前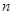 项和,问n取什么值
项和,问n取什么值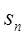 最大。
最大。
已知函数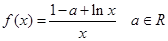 ,
,
(1)求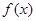 的极值
的极值
(2)若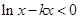 在
在 上恒成立,求
上恒成立,求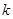 的取值范围
的取值范围
(3)已知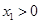 ,
,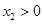 且
且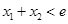 ,求证
,求证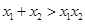
已知函数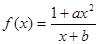
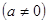 是奇函数,并且函数
是奇函数,并且函数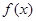 的图象经过点(1,3).
的图象经过点(1,3).
(1)求实数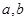 的值;
的值;
(2)求函数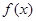 的值域.
的值域.
已知f(x)是实数集R上的函数,且对任意x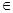 R,f(x)=f(x+1)+f(x-1)恒成立.
R,f(x)=f(x+1)+f(x-1)恒成立.
(1)求证:f(x)是周期函数.
(2)已知f(-4)=2,求f(2012).
盒子内有大小相同的9个球,其中2个红色小球,3个白色小球,4个黑色小球,规定取出1红色小球得到1分, 取出1白色小球得到0分, 取出1个黑色小球得到-1分,现从盒子中任取3个小球。
(1)求取出的3个球颜色互不相同的概率;
(2)求取出的3个球得分之和恰好为1分的概率;
(3)设ξ为取出的3个球中白色球的个数,求ξ的分布列及数学期望.