据预测,我国在“十二五”期间内某产品关税与市场供应量 的关系近似地满足
的关系近似地满足 :
: (其中
(其中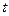 为关税的税率,且
为关税的税率,且 ,
, 为市场价格,
为市场价格,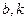 为正常数),当
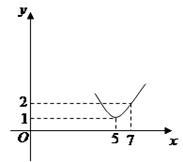
为正常数),当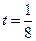 时的市场供应量曲线如图所示;
时的市场供应量曲线如图所示;
(1)根据图象求 的值;
的值;
(2)若市场需求量为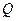 ,它近似满足
,它近似满足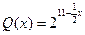 .
.
当 时的市场价格称为均衡价格,为使均衡价格控制在不低于9元的范围内,求税率
时的市场价格称为均衡价格,为使均衡价格控制在不低于9元的范围内,求税率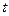 的最小值.
的最小值.
已知函数
(1)求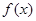 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)已知 是
是 三边长,且
三边长,且 ,
, 的面积
的面积 .求角
.求角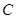 及
及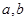 的值.
的值.
已知函数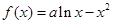 .
.
(1)当 时,求函数
时,求函数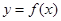 在
在 上的最大值;
上的最大值;
(2)令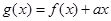 ,若
,若 在区间
在区间 上不单调,求
上不单调,求 的取值范围;
的取值范围;
(3)当 时,函数
时,函数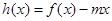 的图像与x轴交于两点
的图像与x轴交于两点 ,且
,且 ,又
,又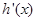 是
是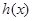 的导函数,若正常数
的导函数,若正常数 满足条件
满足条件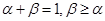 .证明:
.证明: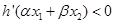 .
.
 的内切圆与三边
的内切圆与三边 的切点分别为
的切点分别为 ,已知
,已知 ,内切圆圆心
,内切圆圆心 ,设点A的轨迹为R.
,设点A的轨迹为R. 
(1)求R的方程;
(2)过点C的动直线m交曲线R于不同的两点M,N,问在x轴上是否存在一定点Q(Q不与C重合),使 恒成立,若求出Q点的坐标,若不存在,说明理由.
恒成立,若求出Q点的坐标,若不存在,说明理由.
如图,正三棱柱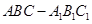 所有棱长都是2,D棱AC的中点,E是
所有棱长都是2,D棱AC的中点,E是 棱的中点,AE交
棱的中点,AE交 于点H.
于点H.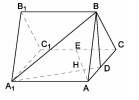
(1)求证: 平面
平面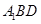 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)求点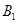 到平面
到平面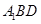 的距离.
的距离.
已知数列 的前
的前 项和为
项和为 ,对一切正整数
,对一切正整数 ,点
,点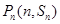 都在函数
都在函数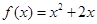 的图像上,且过点
的图像上,且过点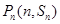 的切线的斜率为
的切线的斜率为 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设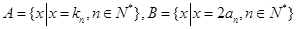 ,等差数列
,等差数列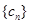 的任一项
的任一项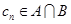 ,其中
,其中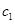 是
是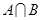 中所有元素的最小数,
中所有元素的最小数,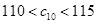 ,求
,求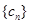 的通项公式.
的通项公式.