直线 经过点
经过点 ,且与圆
,且与圆 相交与
相交与 两点,截得的弦长为
两点,截得的弦长为 ,求
,求 的方程?
的方程?
已知二次函数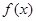 有两个零点
有两个零点 和
和 ,且
,且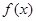 最小值是
最小值是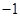 ,函数
,函数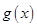 与
与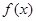 的图象关于原点对称;
的图象关于原点对称;
(1)求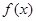 和
和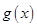 的解析式;
的解析式;
(2)若 在区间
在区间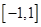 上是增函数,求实数
上是增函数,求实数 的取值范围。
的取值范围。
已知在直角坐标平面内,以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,点 的极坐标是
的极坐标是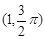 ,曲线C的极坐标方程为
,曲线C的极坐标方程为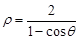 .
.
(I)求点 的直角坐标和曲线C的直角坐标方程;
的直角坐标和曲线C的直角坐标方程;
(II)若经过点 的直线
的直线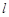 与曲线C交于A、B两点,求
与曲线C交于A、B两点,求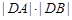 的最小值.
的最小值.
设命题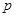 :函数
:函数 是R上的减函数,命题q:
是R上的减函数,命题q: 在
在 上的值域为
上的值域为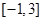 ,若“
,若“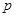 或
或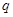 ”为真命题,“
”为真命题,“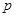 且
且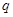 ”为假命题,求实数a的取值范围.
”为假命题,求实数a的取值范围.
已知曲线C的极坐标方程 是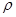 =1,以极点为原点,极轴为
=1,以极点为原点,极轴为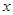 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线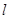 的参数方程为
的参数方程为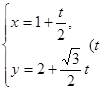 为参数)。
为参数)。
(1)写出直线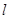 与曲线C的直角坐标方程;
与曲线C的直角坐标方程;
(2)设曲线C经过伸缩变换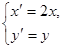 得到曲线
得到曲线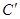 ,设曲线
,设曲线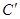 上任一点为
上任一点为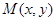 ,求
,求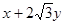 的最小值。
的最小值。
记关于x的不等式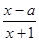 <0 (a>0).的解集为P,不等式|x-1|≤1的解集为Q.
<0 (a>0).的解集为P,不等式|x-1|≤1的解集为Q.
(1)求a=3,求P;
(2)若Q⊆P,求正数a的取值范围.