（本小题满分12分）某人以12．1万元购买了一辆汽车用于上班，每年用于保险费和汽油费共0.9万元，汽车的维修费为：第一年0.2万元，第二年0.4万元，第三年0.6万元，……，依等差数列逐年递增．
（Ⅰ）设使用n年该车的总费用（包括购车费用）为f(n)，试写出f(n)的表达式；
（Ⅱ）求这种汽车使用多少年报废最合算（即该车使用多少年平均费用最少）。
已知向量p＝(an，2n)，q＝(2n＋1，－an＋1)，n∈N*，p与q垂直，且a1＝1.
(1)求数列{an}的通项公式；
(2)若数列{bn}满足bn＝log2an＋1，求数列{an·bn}的前n项和Sn.
在△ABC中，内角A，B，C所对的边分别为a，b，c，且a＝1，c＝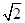
，cos C＝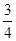
(1)求sin A的值；
(2)求△ABC的面积．
设M是把坐标平面上的点的横坐标伸长到2倍，纵坐标伸长到3倍的伸压变换．
(1)求矩阵M的特征值及相应的特征向量；
(2)求逆矩阵M－1以及椭圆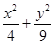
＝1在M－1的作用下的新曲线的方程．
在平面直角坐标系xOy中，已知点A(0,0)，B(－2,0)，C(－2,1)．设k为非零实数，矩阵M＝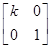
，N＝
，点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1，△A1B1C1的面积是△ABC面积的2倍，求k的值．
．已知矩阵A＝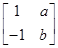
，A的一个特征值λ＝2，其对应的特征向量是α1＝
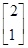.设向量β＝
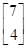，试计算A5β的值．