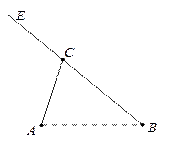
(本小题满分12分) 如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120 km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车 站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.
站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.
(1)计算A,C两站距 离,及B,C两站距离;(2)若甲、乙两车上各有一名旅客需要交换到对方汽车上,问能否在车站C处利用停留时间交换.(3)求10点时甲、乙两车的距离.(可能用到的参考数据:
离,及B,C两站距离;(2)若甲、乙两车上各有一名旅客需要交换到对方汽车上,问能否在车站C处利用停留时间交换.(3)求10点时甲、乙两车的距离.(可能用到的参考数据: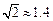 ,
,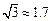 ,
,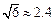 ,
,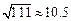 )
)
等差数列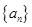 的首项为
的首项为 ,公差
,公差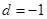 ,前
,前 项和为
项和为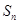 ,其中
,其中 .
.
(Ⅰ)若存在 ,使
,使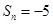 成立,求
成立,求 的值;
的值;
(Ⅱ)是否存在 ,使
,使 对任意大于1的正整数
对任意大于1的正整数 均成立?若存在,求出
均成立?若存在,求出 的值;否则,说明理由.
的值;否则,说明理由.
已知向量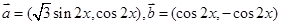 .
.
(Ⅰ)若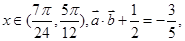 求
求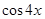 ;
;
(Ⅱ)设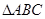 的三边
的三边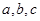 满足
满足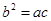 ,且边
,且边 所对应的角为
所对应的角为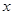 ,若关于
,若关于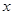 的方程
的方程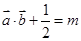 有且仅有一个实数根,求
有且仅有一个实数根,求 的值.
的值.
(本小题满分14分)
已知函数 。
。
(Ⅰ)求函数 的单调区间。
的单调区间。
(Ⅱ)若 上恒成立,求实数
上恒成立,求实数 的取值范围
的取值范围
(Ⅲ)在(Ⅱ)的条件下,对任意的 ,求证:
,求证: 。
。
(本小题满分12分)
已知椭圆C: 的短轴长为
的短轴长为 ,且斜率为
,且斜率为 的直线
的直线 过椭圆C的焦点及点
过椭圆C的焦点及点 。
。
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知一直线 过椭圆C的左焦点
过椭圆C的左焦点 ,交椭圆于点P、Q,
,交椭圆于点P、Q,
(ⅰ)若满足 (
( 为坐标原点),求
为坐标原点),求 的面积;
的面积;
(ⅱ)若直线 与两坐标轴都不垂直,点M在
与两坐标轴都不垂直,点M在 轴上,且使
轴上,且使 为
为 的一条角平分线,则称点M为椭圆C的“左特征点”,求椭圆C的左特征点。
的一条角平分线,则称点M为椭圆C的“左特征点”,求椭圆C的左特征点。
若数列 满足
满足 ,其中
,其中 为常数,则称数列
为常数,则称数列 为等方差数列
为等方差数列
已知等方差数列 满足
满足
求数列 的通项公式;
的通项公式;
(Ⅱ)记 ,则当实数
,则当实数 大于4时,不等式
大于4时,不等式 能否对于一切的
能否对于一切的 恒成立?请说明理由
恒成立?请说明理由