(本题满分16分)设函数y=f(x)对任意实数x，都有f(x)=2f(x+1)，当x∈[0,1]时，f(x)=
x2(1-x).
(Ⅰ)已知n∈N+，当x∈[n,n+1]时，求y=f(x)的解析式；
(Ⅱ)求证：对于任意的n∈N+，当x∈[n,n+1]时，都有|f(x)|≤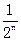
；
(Ⅲ)对于函数y=f(x)
(x∈[0,+∞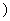
，若在它的图象上存在点P，使经过点P的切线与直线x+y=1平行，那么这样点有多少个？并说明理由
求
在
上的单调递增区间
已知椭圆
的右准线是抛物线的准线，抛物线的顶点是原点，求抛物线方程
已知数列
满足
且
(1) 证明：
；
(2) 比较an与
的大小；
(3) 是否存在正实数c，使得
，对一切
恒成立？若存在，则求出c的取值范围；若不存在，说明理由．
设函数
（Ⅰ）求曲线
在点
处的切线方程；
（Ⅱ）求函数
的单调区间；
（Ⅲ）若函数在区间
内单调递
增，求
的取值范围.
（本小题满分12分）已知A（1，f′(1)）是函数y=f(x)的导函数图像上的一点，点B的坐标为(x,㏑(x+1))，向量
=(1,1)，设f(x)=
·
(1)求函数y=f(x)的表达式;
(2)若x∈[-1,1]时，不等式
x
≤f(x)+m-
m-3都恒成立，求实数m的取值范围.