已知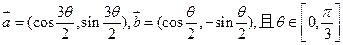
(1)求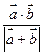 的最值; (2)是否存在
的最值; (2)是否存在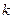 的值使
的值使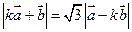 ?
?
已知二次函数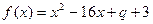 。
。
(1)若函数在区间[-1,1]上存在零点,求实数q的取值范围;
(2)问是否存在常数t(t≥0),当x∈[t,10]时,f(x)的最大值与最小值之差为12-t。
函数y=f(x)(x≠0)是奇函数,且当x∈(0,+∞)时为增函数,且f(1)=0。
(1)求关于t的方程f(2t+5)=0的解;
(2)求不等式f[x(x-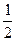 )]<0的解集。
)]<0的解集。
已知△ABC是边长为2的正三角形,如图,P,Q依次是AB,AC边上的点,且线段PQ将△ABC分成面积相等的两部分,设AP=x,AQ=t,PQ=y,求: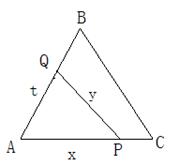
(1)t关于x的函数关系式;
(2)y关于x的函数关系式;
(3)y的最小值和最大值。
已知函数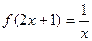
(1)求f(x);
(2)求f(x)在区间[2,6]上的最大值和最小值。
已知集合
(1)当m=3时,求 ;
;
(2)若 ,求实数m的值。
,求实数m的值。