如图,在五面体ABCDEF中,FA  平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE=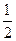 AD
AD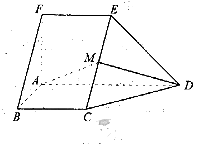
(1)证明平面AMD 平面CDE;
平面CDE;
(2)求二面角A-CD-E的余弦值
已知
的角
、
、
所对的边分别是
、
、
,设向量
,
,
.
(1)若
,求证:
为等腰三角形;
(2)若
,边长
,角
,求
的面积.
设函数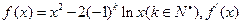 表示f(x)导函数。
表示f(x)导函数。
(I)求函数一份(x))的单调递增区间;
(Ⅱ)当k为偶数时,数列{ }满足
}满足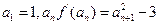 .证明:数列{
.证明:数列{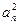 }中
}中
不存在成等差数列的三项;
(Ⅲ)当后为奇数时,证明:对任意正整数,n都有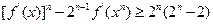 成立.
成立.
已知双曲线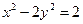 的左、右两个焦点为
的左、右两个焦点为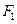 ,
,  ,动点P满
,动点P满
足|P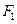 |+| P
|+| P |=4.
|=4.
(I)求动点P的轨迹E的方程;
(1I)设过 且不垂直于坐标轴的动直线l交轨迹E于A、B两点,问:终段O
且不垂直于坐标轴的动直线l交轨迹E于A、B两点,问:终段O
上是否存在一点D,使得以DA、DB为邻边的平行四边形为菱形?作出判断并证明.
某中学组建了A、B、C、D、E五个不同的社团组织,为培养学生的兴趣爱好,要求每个学生必须参加,且只能参加一个社团.假定某班级的甲、乙、丙三名学生对这五个社团的选择是等可能的.
(I)求甲、乙、丙三名学生参加五个社团的所有选法种数;
(Ⅱ)求甲、乙、丙三人中至少有两人参加同一社团的概率;
(Ⅲ)设随机变量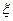 为甲、乙、丙这三个学生参加A社团的人数,求
为甲、乙、丙这三个学生参加A社团的人数,求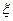 的分布列与
的分布列与
数学期望.